
On the previous page, we saw that the following is a correct solution using two bounded buffers:

We will call this a symmetric solution because threads in both groups follow the same steps except for the uses of different variables. We certainly can make a copy of the producer/consumer program and set the number of slots to 1. However, this would be an overkill. Our goal is to convert this symmetric solution to use semaphores only.
To implement PUT() for buffer Buf_A, we need a semaphore NotFull_A with an initial value 1 because the buffer is initially not full. We also need a second semaphore NotEmpty_A, with initial value 0, for a consumer to wait on. We do not need another lock to protect the buffer because the existing binary semaphores Amutex and Bmutex serve the same purpose. The converted program is shown below. A thread A first enters its critical section so that it is the only thread in group A that can perform a message exchange. Then, thread A waits for the buffer being not full, fills it with the message, and signals the consumer (i.e., a thread in group B) telling it that the buffer is filled with a message. This ends the first stage in which thread A serves as a producer. In the second stage, thread A executes GET() and becomes a consumer. Thus, thread A waits for buffer Buf_B being not empty, retrieves the message, stores it into local variable Var_A, and signals a producer (i.e., a thread in group B that is about to execute its PUT() call) so that a new message can be filled into buffer Buf_B. This completes A's message exchange cycle and releases the critical section lock Amutex. Because the solution is symmetric, a thread in group B essentially does the same thing except for the use of different variables.
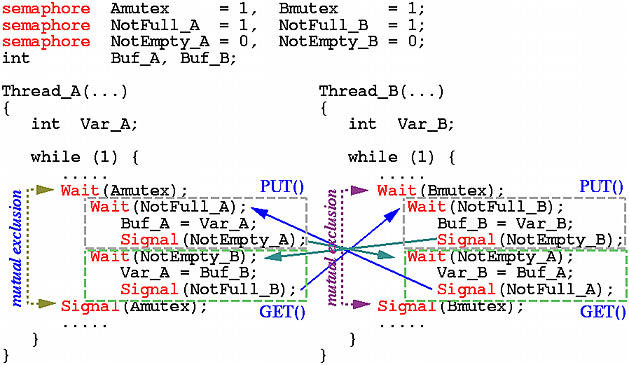
Why must a solution symmetric? What if we insist that the message exchange protocol must be (1) A deposits his message, (2) B retrieves the message, (3) B deposits its message, and (4) A retrieves the message? In this way, threads in group A are active and threads in group B are passive. Based on this idea, we have the following non-symmetric version:

With this version, the message exchange is serialized into the sequence of PUT() by A, GET() by B, PUT() by B, and GET() by A. More precisely, the message exchange section is not run in parallel, and is always executed in the specified order. Is this version correct? Yes, it is and its correctness can be shown essentially the same way we did for the symmetric version.
Let us remove the use of the bounded buffer and its PUT() and GET() calls. Because the serialized sequence, we do not need two buffer variables. We can use one shared variable Shared. When threads A and B put messages, the messages go into variable Shared, and when threads A and B get messages, they take from variable Shared. Thus, we have our first simplification. Because of this simplification, we need one semaphore NotFull, with initial value 1, to control if this shared buffer Shared is full or not, and we have our second simplification. However, we cannot eliminate semaphores NotEmpty_A and NotEmpty_B, because they are needed to inform threads A and B that the buffer is not empty (i.e., the buffer has a message). Once these two simplifications are implemented, we have the following program:

Where are the semaphores Amutex and Bmutex? In fact, we do not need them any more. Semaphore NotFull serves the purpose of Amutex. Since the initial value of NotEmpty_A is 0, any thread B that reaches the Wait() is blocked until a thread A in its critical section signals semaphore NotEmpty_A. Once a thread B passes through semaphore NotEmpty_A, it is the only thread between the wait/signal pair. This is not difficult to see. Semaphore NotEmpty_A is only signaled by thread A that is in its critical section. However, right after this signal, that thread is blocked by Wait(NotEmpty_B) until a thread B signals it. At this point, thread B has already completed its message exchange and is ready to leave the critical section. Consequently, no more than one thread in group B can be between the wait/signal pair.
Both correct solutions, especially the non-symmetric one, are no more complex than the incorrect ones. The symmetric version has six statements in each critical section, and the non-symmetric one has four in Thread_A()'s critical section and two in Thread_B()'s. However, because the statements in the non-symmetric version are executed sequentially, there are exactly six statements. Hence, in terms of statements count, both versions are similar.
Since the symmetric solution has three waits and non-symmetric one has only two, in terms of synchronization efficiency, the non-symmetric version is better. On the other hand, since the message exchange sections are identical in both thread groups, the symmetric version may be easier to understand.


|

|

|