Basic Concept

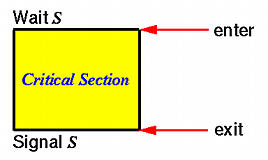
Semaphores, another important contribution by E. W. Dijkstra, can be viewed as an extension to mutex locks. A semaphore is an object with two methods Wait and Signal, a private integer counter and a private queue (of threads). The semantics of a semaphore is very simple. Suppose S is a semaphore whose private counter has been initialized to a non-negative integer.

When Wait is executed by a thread, we have two possibilities:
- The counter of S is positive
  In this case, the counter is decreased by 1 and the thread resumes its execution.
- The counter of S is zero
  In this case, the thread is suspended and put into the private queue of S.
When Signal is executed by a thread, we also have two possibilities:
- The queue of S has no waiting thread
  The counter of S is increased by one and the thread resumes its execution.
- The queue of S has waiting threads
  In this case, the counter of S must be zero (see the discussion of Wait above). One of the waiting threads will be allowed to leave the queue and resume its execution. The thread that executes Signal also continues.

The operations of Wait or Signal are atomic. This means once the activities of Wait start (i.e., testing and decreasing the value of the counter and putting the thread into the queue), they will continue to the end without any interruption. More precisely, even though there are many steps to carry out Wait and Signal, these steps are considered as a single non-interruptible instruction. Similarly, the same applies to Signal. Moreover, if more than one threads try to execute Wait (or Signal), only one of them will succeed. We should not make any assumption about which thread will succeed.
Because Wait may cause a thread to block (i.e., when the counter is zero), it has a similar effect of the lock operation of a mutex lock. Similarly, a Signal may release a waiting threads, and is similar to the unlock operation. In fact, semaphores can be used as mutex locks. Consider a semaphore S with initial value 1. Then, Wait and Signal correspond to lock and unlock:

Let us examine how this pair of Wait and Signal can guarantee mutual exclusion. Keep in mind that the initial value of the counter of S is 1. Suppose a number of threads try to execution Wait. Because there is only one thread can successfully execute Wait, this thread, say A, causes the counter to be decreased by 1, and enters the critical section. Since the initial value of the counter is 1, once thread A enters the critical section, the counter becomes 0, and, as a result, all subsequent attempts in executing Wait will be blocked. Therefore, this justifies our claim that Wait is similar to lock.
When thread A exits the critical section, it executes Signal. If there are waiting threads, one of them will be released, and this released thread enters the critical section. Note that the counter is still zero (because, in this case, Signal does not increase and Wait does not decrease the counter), which means all subsequent threads that try to execute Wait are blocked. On the other hand, if there is no waiting threads, the execution of Signal causes the value of the counter to be increased by 1, making its current value 1. In this case, the next thread that executes Wait can enter the critical section. Therefore, Signal is similar to unlock.
In summary, we learn that setting the counter to 1 initially will guarantee that at most one thread can be in the critical section, if all involving threads follow the same Wait-Signal sequence.
If you are careful, you will see that the value of the counter is either 1 or 0, and never has any other value. Therefore, it is referred to as a binary semaphore. If we replace the counter with a Boolean variable and interpret 1 and 0 as true (i.e., lock is open) and false (i.e., lock is closed), respectively, then a binary semaphore becomes a mutex lock! Therefore, you can use mutex lock or binary semaphore interchangeably.
However, the beauty of using semaphores is that the initial value does not have to be 1. It could be any non-negative value. Later on we will discuss other techniques of using semaphores.