The Law of Cosines in Euclid's Elements

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 18, 2025

Euclid's Elements was written c. 300 BC. Note that trigonometry was not able for Euclid to use for sure, and Euclid and his contemperaries used lengths and areas. Consequently, the statements can be rather long and not easy to understand.

There are at least three propositions related to the proofs to the Pythagorean Theorem. The first one is in Book 1 Proposition 47 using rectangle areas, which is commonly seen one and will be discussed on this page. The second one did not prove the Pythagorean Theorem based on similar triangles, but it paved the way to offer a very simple proof of the Pythagorean Theorem. This proof is presented in Book 6 Proposition 8. I am a little bit puzzled because Euclid only proved the Pythagorean Theorem using area. However, this proof based on similar triangles was very popular in elementtary geometry textbooks published in the 19th century. For example, please Adrien-Marie Legendre's Éléments de Géométrie. The third proof is a generalization of the Pythagorean Theorem in Book 6 Proposition 31 which is not the focus of our discussion here.

Let us talk about the second proof first. The following is Book 6 Proposition 8:

If in a right-angled triangle a perpendicular be drawn from the right angle to the base, the triangles adjoining the perpendicular are similar both to the whole and to one another.

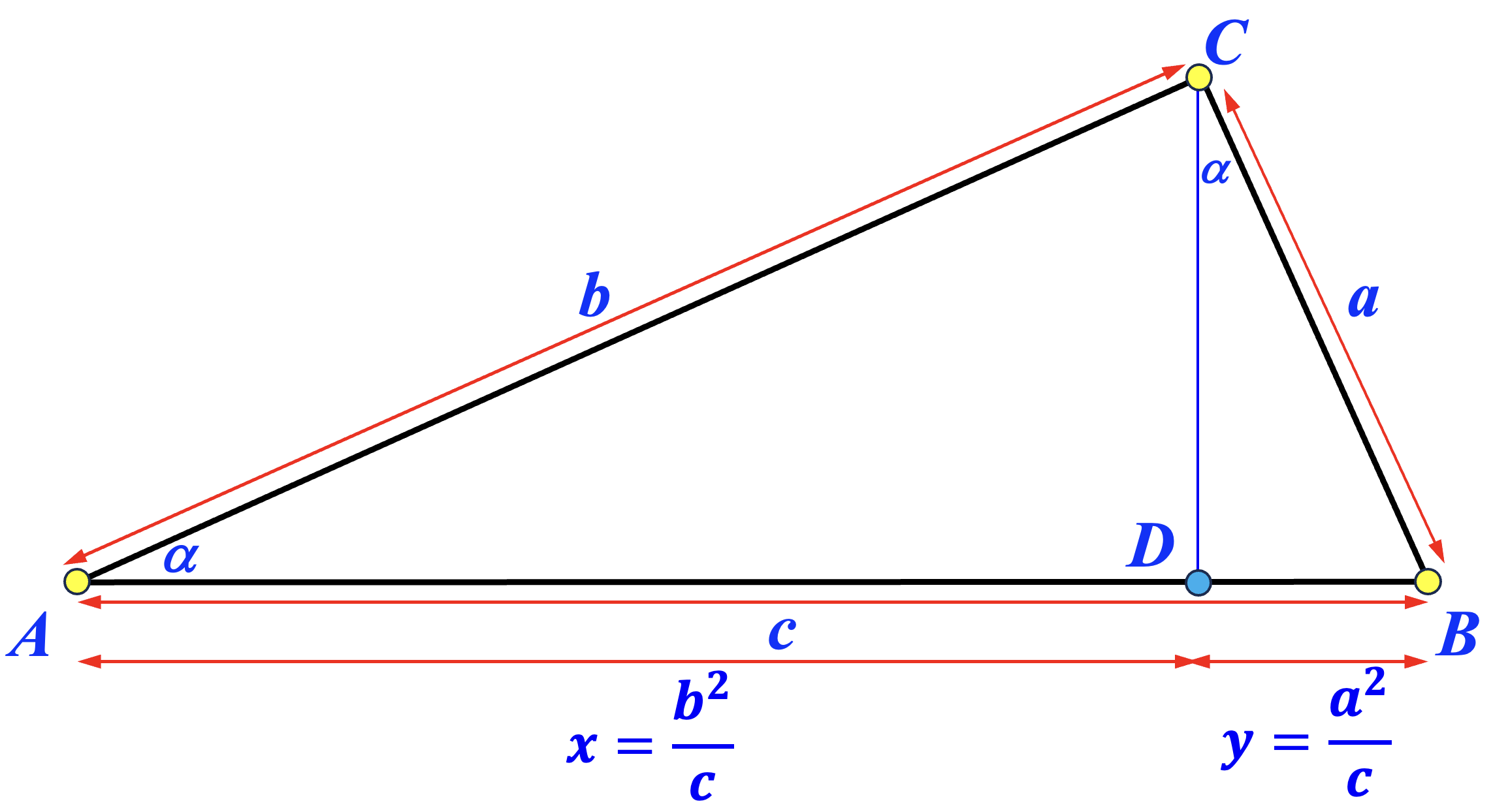
This means that in the diagram below right triangles $ \bigtriangleup ABC $, $ \bigtriangleup CBD $ and $ \bigtriangleup ACD $ are similar, where $ D $ is the perpendicular foot from $ C $ to the hypotenuse. Let $ x = \overline{AD} $ and let $ y = \overline{DB} $. Because $ \bigtriangleup ABC $ is similar to $ \bigtriangleup ACD $, we have $ \frac{x}{b} = \frac{b}{c} $ and hence $x = \frac{b^2}{c} $. Because $ \bigtriangleup ABC $ is similar to $ \bigtriangleup CBD $, we have $ \frac{y}{a} = \frac{a}{c} $ and hence $y = \frac{a^2}{c} $. Then, we have \[ c = x+y = \frac{b^2}{c} + \frac{a^2}{c} = \frac{a^2+b^2}{c} \] Simplifying gives the Pythagorean Theorem. This is Proof One in Loomis' book The Pythagorean Proposition (page 24). Loomis gave the credit to Adrien-Marie Legendre and said This is the shortest proof possible of the Pythagorean Proposition.

Euclid's Elements Book 6 Proposition 8

The first proof using areas is more interesting and closely related to our topic here. In fact, in Book 2 we find two propositions as follows:

Proposition 12
In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle con- tained by one of the sides about the obtuse angle, namely that on which the perpendic- ular falls, and the straight line cut off outside by the perpendicular towards the obtuse.

Proposition 13
In acute-angled triangles the square on the side subtending the acute angle is less than the squares on the sides containing the acute angle by twice the rectangle contained by one of the sides about the acute angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the acute angle.

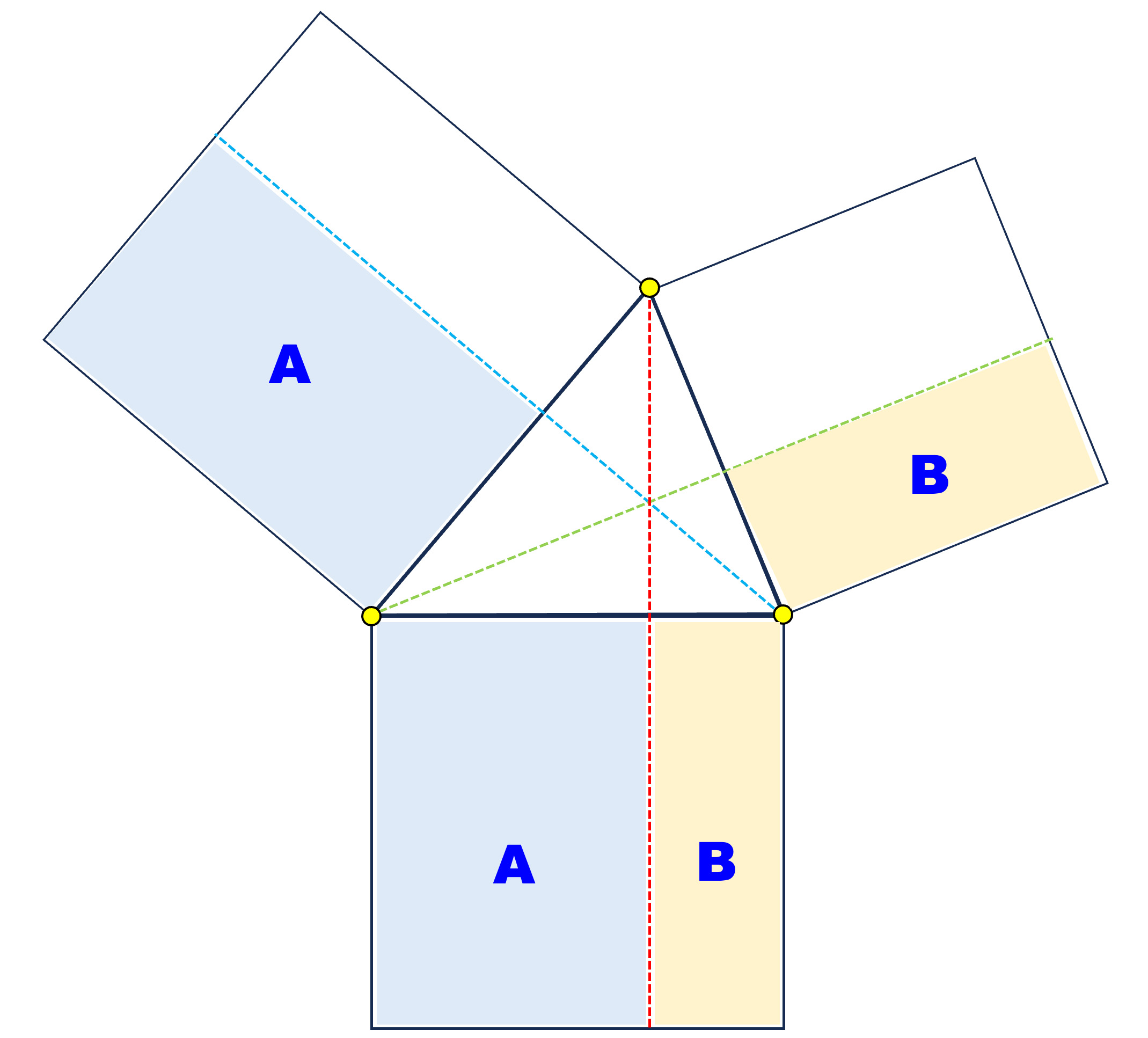
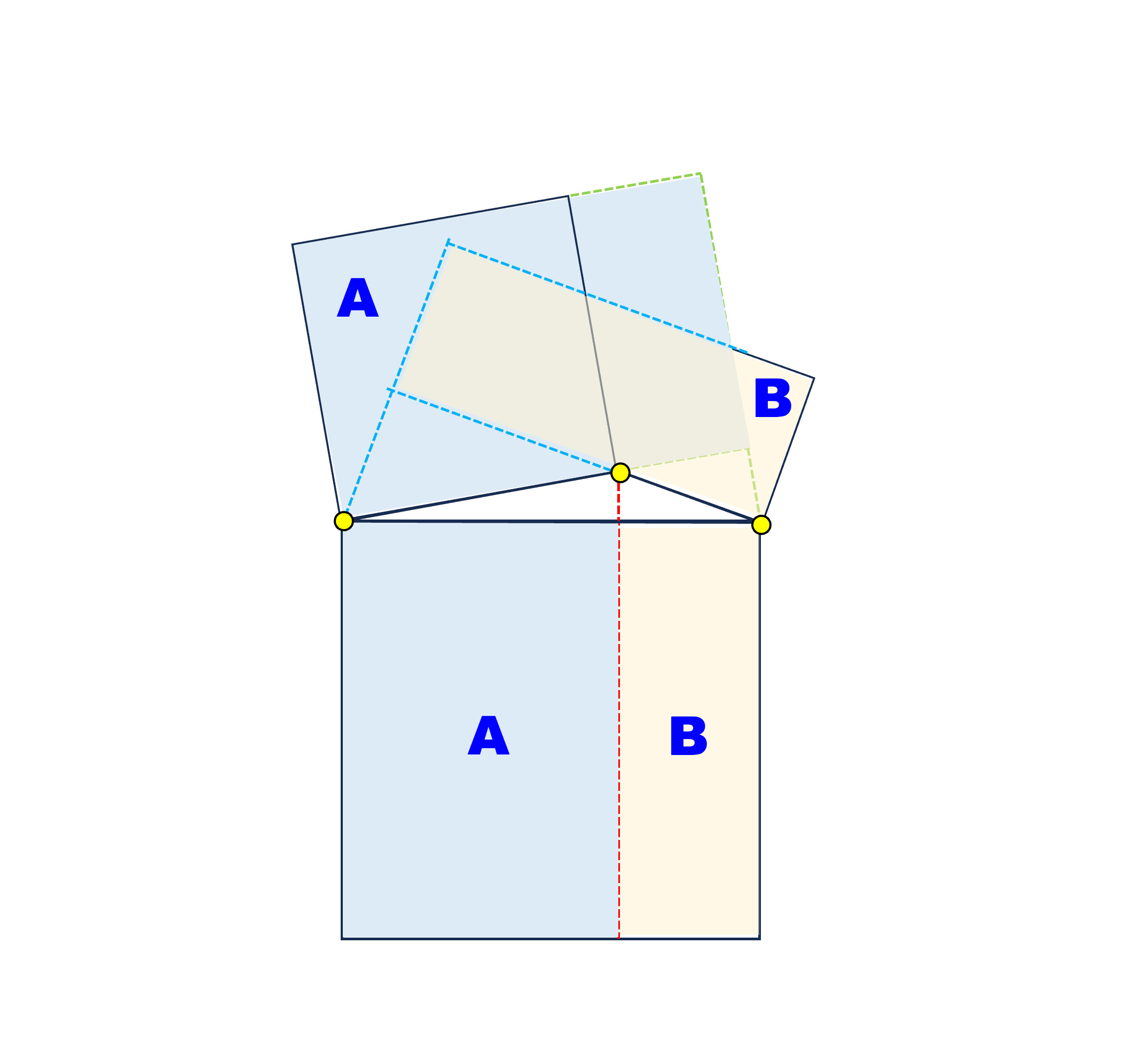
The main difference between the two cases is the greater than in the former and the less than in the latter. The diagrams below illustrate what these two propositions state. From each vertex drop a perpendicular to its opposite side. This line cuts the square on the opposite side into two rectangles. If all angles are acute, each of the three squares are divided into two smaller rectangles both being subsets of the containing one (left diagram below. Furthermore, the two rectangles sharing a common (triangle) vertex have the same area. If the triangle has an obtuse angle (right diagram below), the situation is different. In this case, the perpendicular from a vertex whose angle is not obtuse to its opposite side is outside of the triangle, and the division of the square on the opposite side is also outside of the square. The rectangles sharing a common vertex still have the same area. Each of these two rectangles has one side the same as the square and the opposite vertex of this rectangle is the perpendicular foot from a triangle vertex to the far side of the rectangle.

The Acute Angle Case

The Obtuse Angle Case

These are actually the Law of Cosines stated in geometric terms (i.e., areas). However, Euclid proved both propositions using the Pythagorean Theorem, even though the technique used in the proof of the Pythagorean Theorem can be applied to prove both propositions with minimal effort.
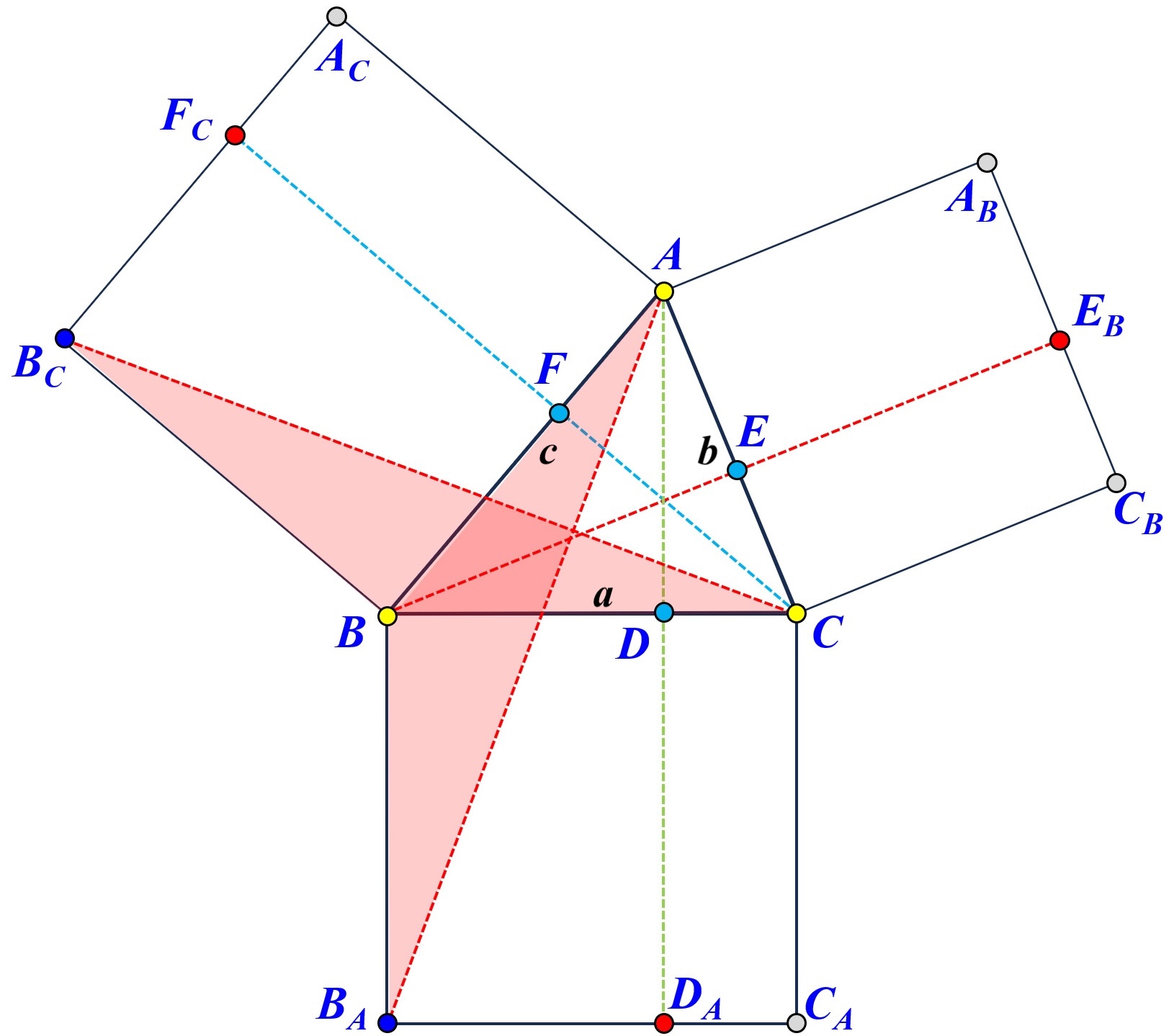
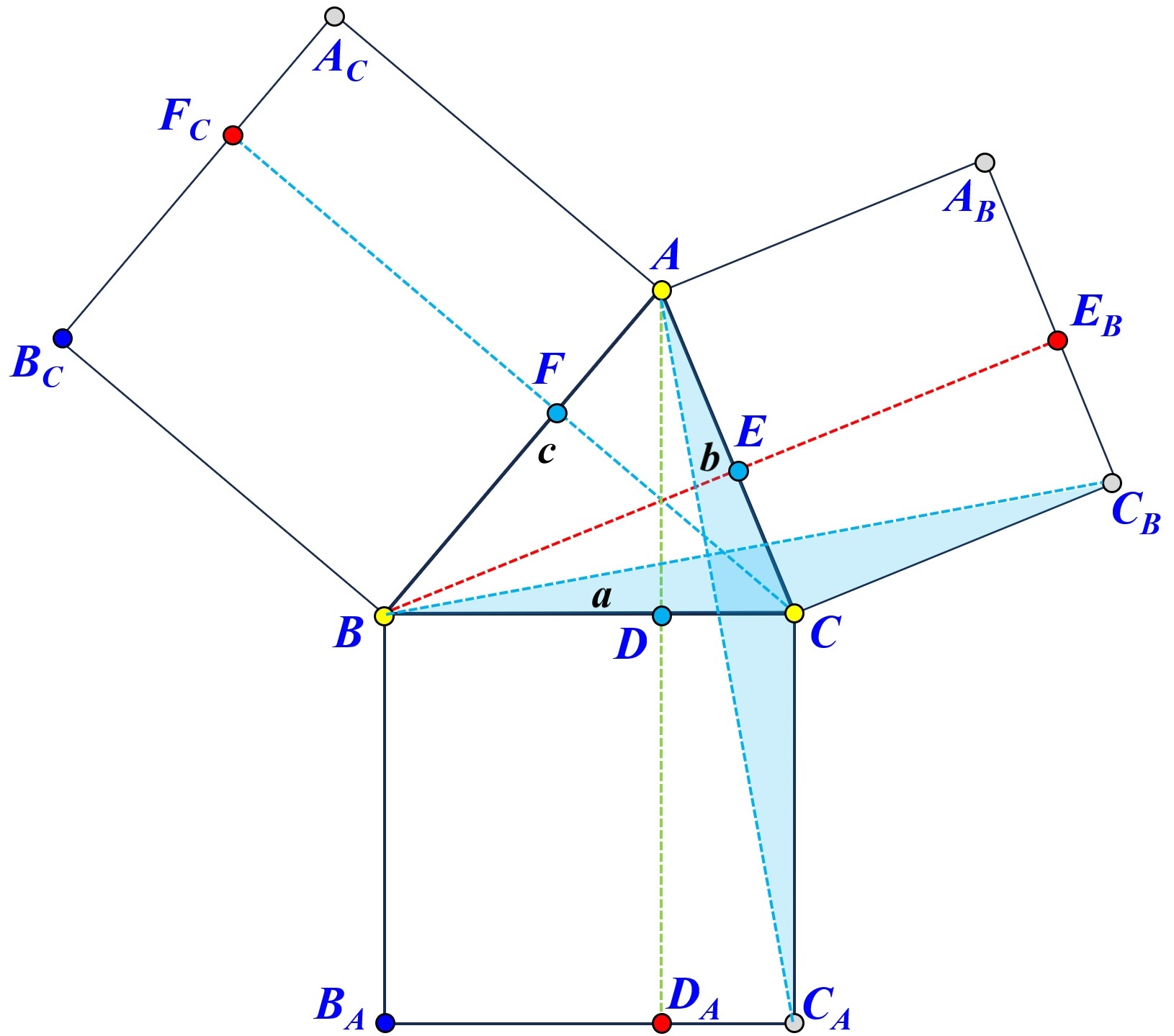
Consider the acute angle $ \angle A $ case first. From each vertex drop a perpendicular to its opposite side. Each perpendicular meets the opposite side of the vertex and the far side of the square (see diagrams below). For example, the perpendicular from $ A $ to its opposite side $ \overleftrightarrow{BC} $ meets it at $ D $ and the opposite side of the square on $ \overleftrightarrow{BC} $ at $ D_A $. Do the same for $ B $ and $ C $.

Acute Angle: Three Pairs of Scissors

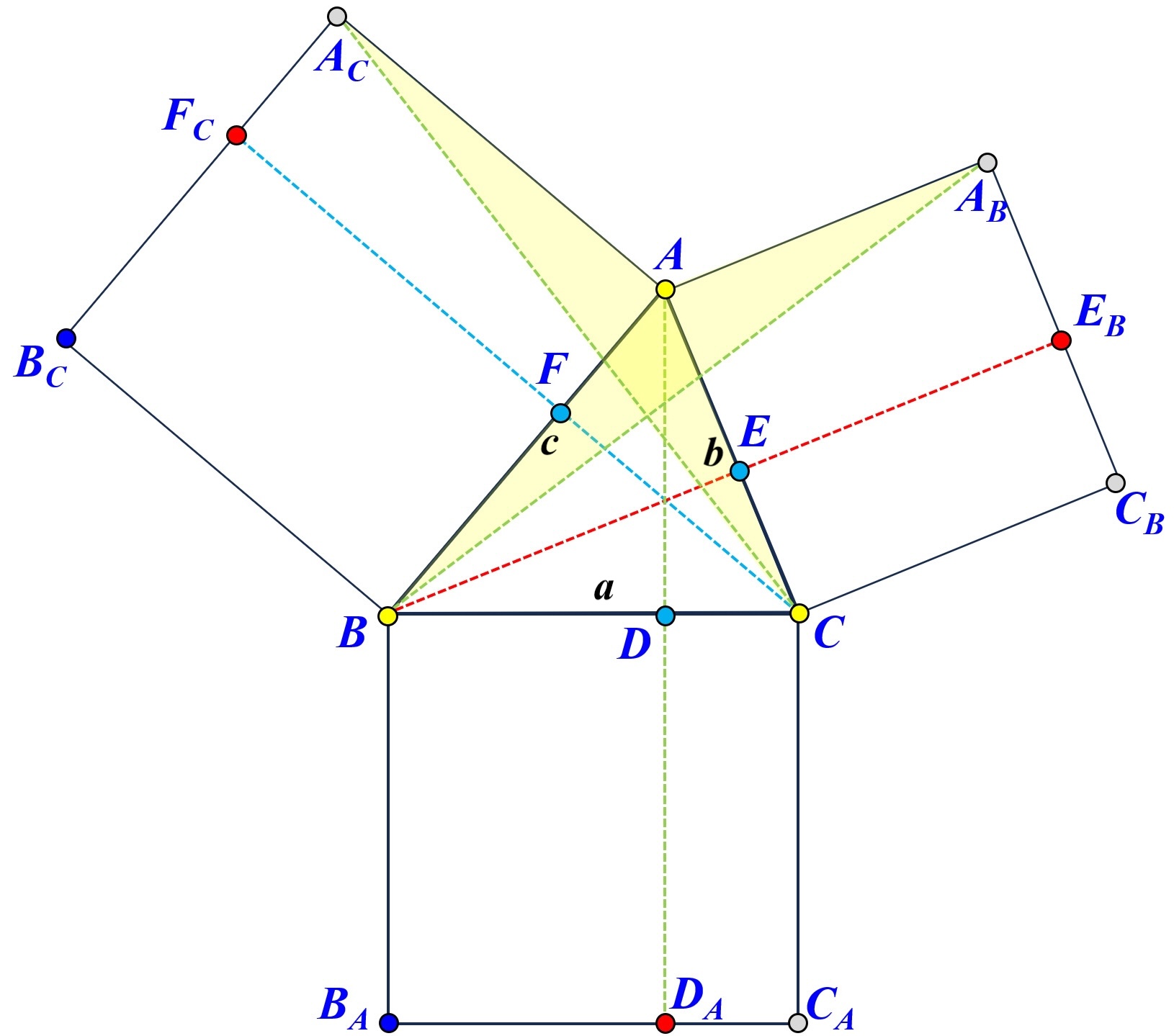
Each vertex has a pair of scissors of triangles marked in the same color. These two triangles share the same vertex of the triangle and have one edge from each of its two adjacent squares. Hence, the two triangles in each pair are congruent with each other and have the same area. This implies that the two rectangles sharing the same vertex have the same area. Consequently, we have $$ \begin{eqnarray*} a^2 &=& \mbox{Area}(BCC_AB_A) \\ &=& \mbox{Area}(BDD_AB_A) + \mbox{Area}(DCC_AD_A) \\ &=& \mbox{Area}(BFF_CB_C) + \mbox{Area}(CEE_BC_B) \\ &=& \left( \mbox{Area}(BAA_CB_C) - \mbox{Area}(FAA_CF_C) \right) + \left( \mbox{Area}(CAA_BC_B) - \mbox{Area}(EAA_BE_B) \right) \\ &=& \mbox{Area}(BAA_CB_C) + \mbox{Area}(CAA_BC_B) - \left ( \mbox{Area}(FAA_CF_C) + \mbox{Area}(EAA_BE_B) \right) \\ &=& c^2 + b^2 - 2\cdot\mbox{Area}(FAA_CF_C) \\ &\mbox{or}& c^2 + b^2 - 2\cdot\mbox{Area}(EAA_BE_B) \end{eqnarray*} $$
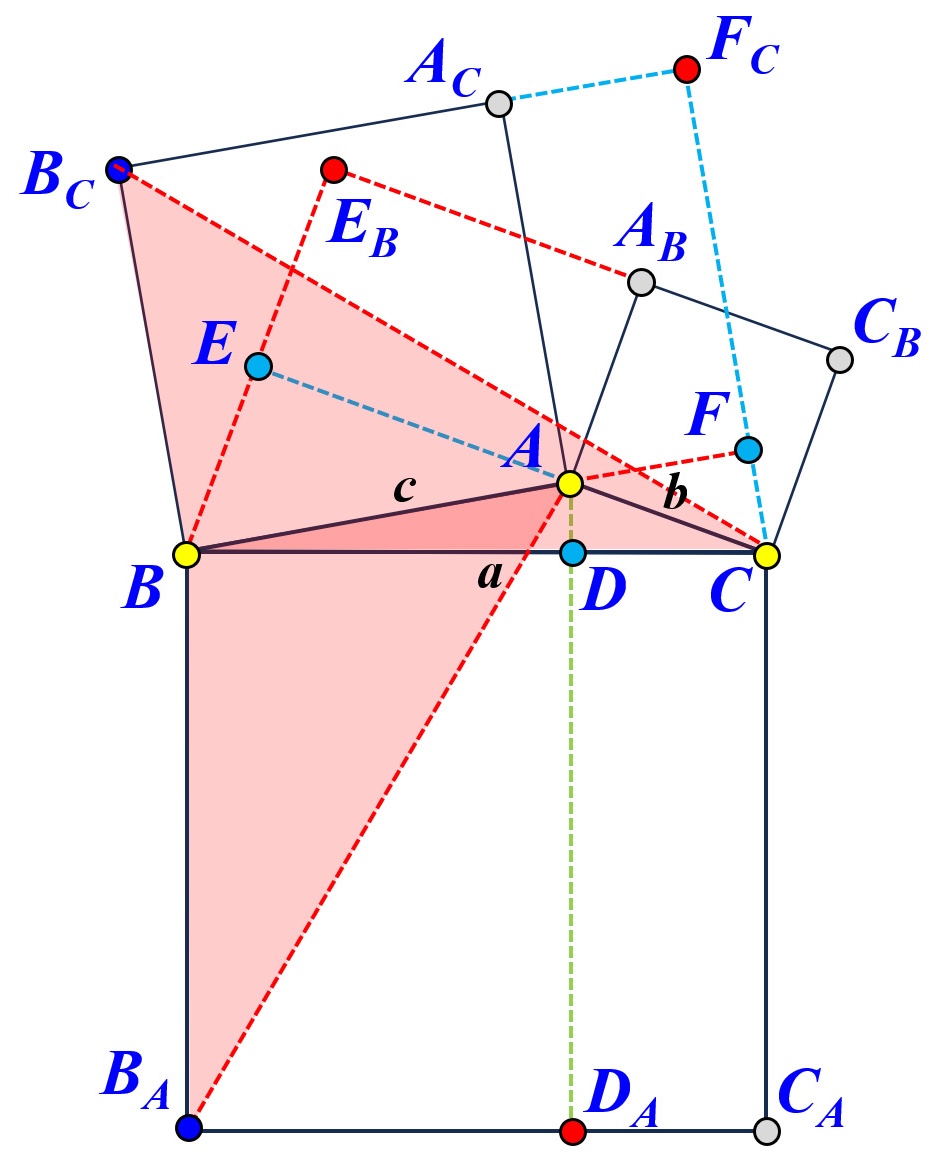
The obtuse angle case works exactly the same way with one exception.

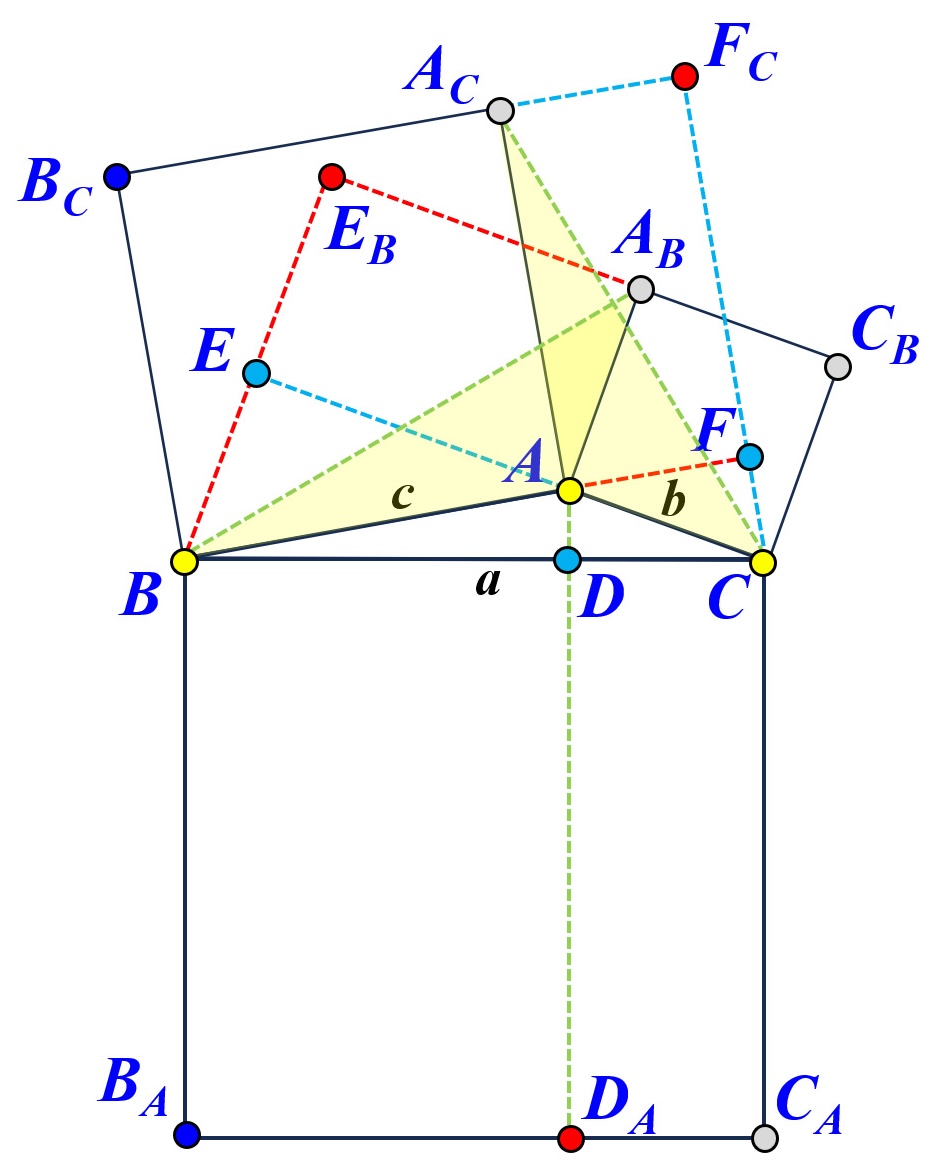
Obtuse Angle: Three Pairs of Scissors

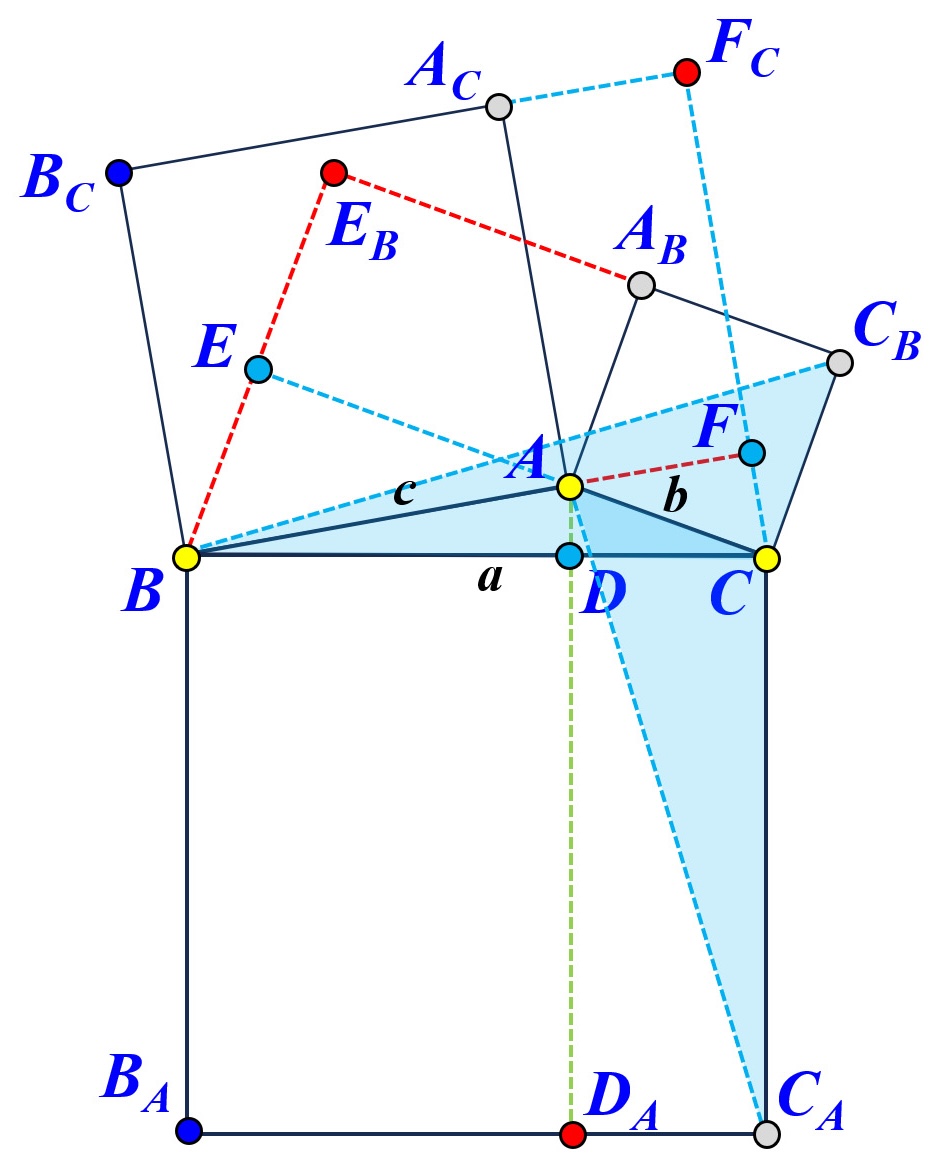
Because the division lines are outside of the square for the sides opposite to the two acute angles, the subtraction signs in the above must be changed to addition signs as follows: $$ \begin{eqnarray*} a^2 &=& \mbox{Area}(BCC_AB_A) \\ &=& \mbox{Area}(BDD_AB_A) + \mbox{Area}(DCC_AD_A) \\ &=& \mbox{Area}(BFF_CB_C) + \mbox{Area}(CEE_BC_B) \\ &=& \left( \mbox{Area}(BAA_CB_C) + \mbox{Area}(FAA_CF_C) \right) + \left( \mbox{Area}(CAA_BC_B) + \mbox{Area}(EAA_BE_B) \right) \\ &=& \mbox{Area}(BAA_CB_C) + \mbox{Area}(CAA_BC_B) + \left ( \mbox{Area}(FAA_CF_C) + \mbox{Area}(EAA_BE_B) \right) \\ &=& c^2 + b^2 + 2\cdot\mbox{Area}(FAA_CF_C) \\ &\mbox{or}& c^2 + b^2 + 2\cdot\mbox{Area}(EAA_BE_B) \end{eqnarray*} $$
In this way, we proved the acute angle case and the obtuse case. The obtained forms are similar to the Law of Cosines in the last term. Because trigonometry was not available to Euclid, what Euclid can do is expressing the results using areas. However, converting the above to using trigonometry is an easy task.
Now return to the acute angle case. $ \mbox{Area}(EAA_BE_B) $ is computed as $ \overline{AF}\times\overline{AA_C} =c\times\overline{AF}$. In triangle $ \bigtriangleup ACF $ we have $ \overline{AF} = \overline{AC}\cdot\cos(A) = b\cdot\cos(A) $. Therefore, the Law of Cosines for a triangle of all acutae angles holds: \[ a^2 = b^2 + c^2 -2bc\cos(A) \]
The obtuse case is similar except that $ F $ is outside of the segment $ \overline{AB} $. In this case $ \overline{AF} = b\cdot\cos(\angle CAF) = b\cdot\cos(180^{\circ}-A) = -b\cdot\cos(A) $. Plugging the above into the result for the obtuse case yields the Law of Cosines.
In this way, the Law of Cosines is proved without using the Pythagorean Theorem nor the Pythagorean Identity. Let me remind you again that trigonometry was not available to Euclid and that Euclid proved Book 2 Proposition 12 and Proposition 13 using the Pythagorean Theorem.
If $ \angle A = 90^{\circ} $, we have the Pythagorean Theorem.
Could Euclid Be the First Person Who Proved the Pythagorean Theorem Using Trigonometry?
In Book 1 Proposition 47, Euclid provided exactly the same proof as shown above. If $ \angle A = 90^{\circ} $, then $ \mbox{Area}(AFF_CA_C) = \mbox{Area}(AEE_BA_B) = 0 $ and only the scissors at $ \angle B $ and the scissors $ \angle C $ are used. So, we may think what Euclid did was providing an algorithm to prove the Pythagorean Theorem, and this algorithm can be used to prove Book 2 Proposition 12 and Proposition 13 without any modifications (i.e., just applying it to all vertices). Sir Thomas L. Heath in his book The Thirteen Books of Euclid’s Element, Volume 1, page 404 stated the following:
Since in this proposition and the next we have to do with the squares on the sides of triangles, the particular form of graphic representation of areas which we have had in Book II. up to this point does not help us to visualize the results of the propositions in the same way, and only two lines of proof are possible, (1) by means of the results of certain earlier propositions on Book II. combined with the results of I. 47, and (2) by means of the procedure in Euclid’s proof of I. 47 itself. The alternative proofs of II. 12, 13 after the manner of Euclid’s proof I. 47 are therefore alone worth giving.

This is what a mathematician should remember. Yes, Euclid did not prove Book 2 Proposition 12 and Proposition 13 in the above way. Instead Euclid did use the Pythagorean Theorem. However, the procedure (or algorithm) in the proofs of the mentioned above can be applied to the proof of the Pythagorean Theorem. Shouldn't we give the credit of proving the Law of Cosines without using the Pythagorean Theorem or the Pythagorean Identity to Euclid?
No, I am not a mathematician and I am a compueter scientist. In the history of computing, the algorithms are more important than simply proofs. In my mind, Euclid's algorithm DID provide a proof of the Law of Cosines using trigonometry even though Euclid did not have trigonometry in his hands.
Go back to Home Page.