Lengvárszky's Proof of the Pythagorean Theorem (2018)

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 21, 2025

in 2018 Lengvárszky published a proof of the Pythagorean Theorem using the angle difference and angle sum identities for the tangent function. This is at least four years earlier than Jackson-Johnson's 2023 impossible proof. So far, we have seen several impossible proofs that are earlier than the one by Jackson-Johnson. Here you can find a copy of Lengvárszky's paper.

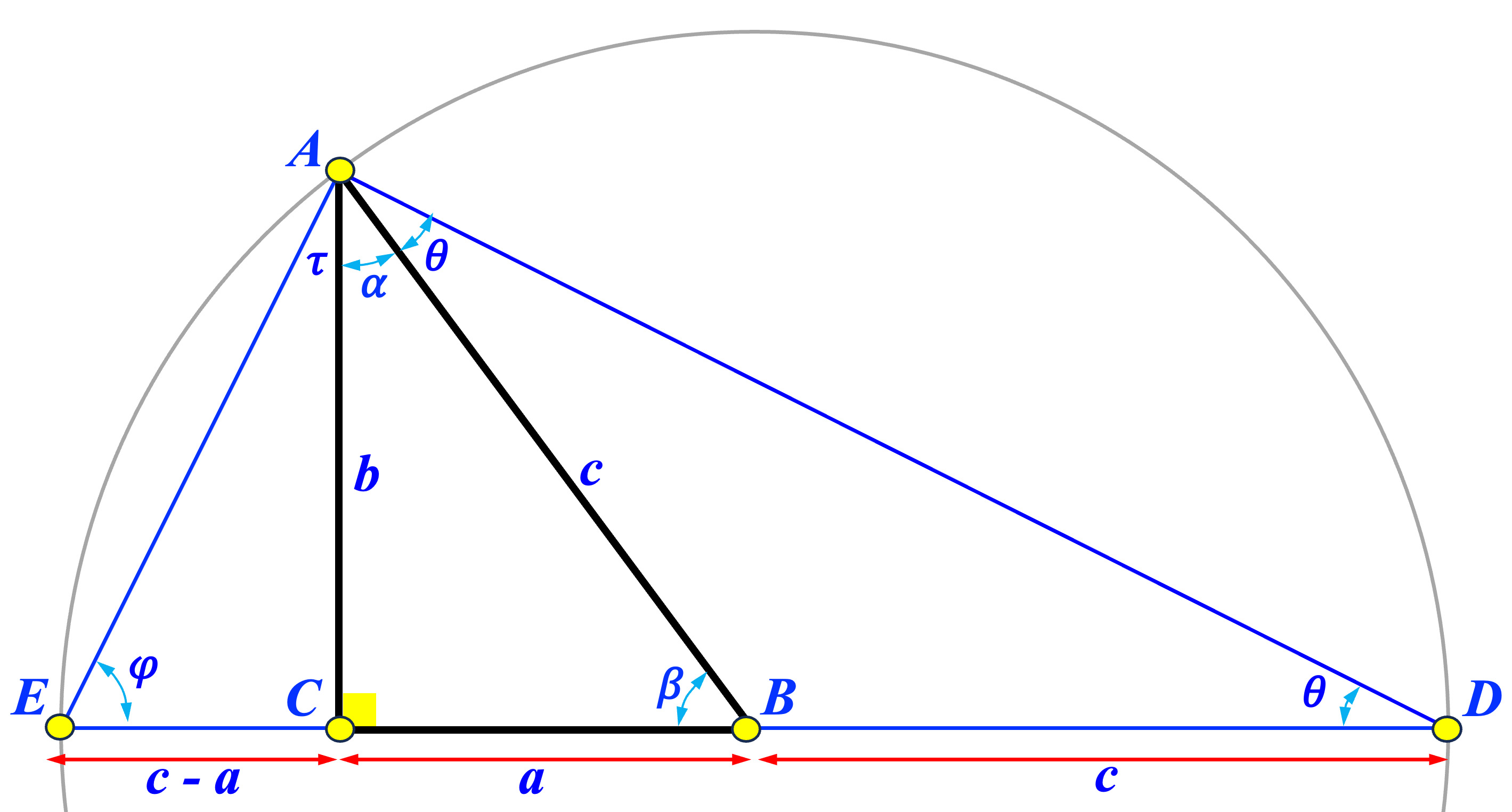
We look at the use of the angle sum identity first. Let \( \bigtriangleup ABC \) be a right triangle with \( \angle C = 90^{\circ} \), \( \angle A = \alpha \) and side lengths \( a \), \( b \) and \( c \) as shown in the diagram below. Let the circle with center \( B \) and radius \( c = \overline{AB} \) meet \( \overleftrightarrow{BC} \) at \( E \) and \( D \) as shown. Then, we have the following: \[ \overline{EC} = c-a, \mbox{\ \ \ \ \ \ \ \ \ \ } \overline{DC} = c+a, \mbox{\ \ \ \ \ \ \ \ \ \ } \angle BAD = \angle BDA = \theta \mbox{\ \ \ \ \ \ \ \ \ \ and\ \ \ \ \ \ \ \ \ } \varphi = \angle ECA = \alpha + \theta \] Now we apply the angle sum identity for the tangent function: \[ \frac{c-a}{b}=\tan(\alpha+\theta)= \frac{\tan(\alpha)+\tan(\theta)}{1-\tan(\alpha)\cdot\tan(\theta)} = \frac{\frac{a}{b}+\frac{b}{a+c}}{1-\frac{a}{b}\cdot\frac{b}{a+c}} \] Simplifying yields the Pythagorean Theorem.

We shall turn to a proof of the Pythagorean Theorem using the angle difference identity for the tangent function. We shall use the diagram above again. First, note the following relation: \[ \tau = \angle EAC = 90^{\circ}-(\alpha + \theta) = \theta \] Because \( \varphi = \alpha + \theta \), we have \( \tau = \theta = \varphi-\alpha \). Now applying the angle difference identity for the tangent function gives \[ \frac{c-a}{b}=\tan(\varphi-\alpha)=\frac{\tan(\varphi)-\tan(\alpha)}{1+\tan(\varphi)\cdot\tan(\alpha)} = \frac{\frac{b}{c-a}-\frac{a}{b}}{1+\frac{b}{c-a}\cdot\frac{a}{b}} \] Simplifying yields the Pythagorean Theorem.

So, we just proved that the angle sum and angle difference identities for the tangent function can be used to prove the Pythagorean Theorem. Additionally, the proofs are rather simple, actually simpler than Jackson-Johnson's 2023 proof.

Go back to Home Page.