Luzia's 2015 Proof

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 18, 2025

Nuno Luzia has a proof in an 2015 unpublished manuscript available here. This preprint actually includes two proofs, one of which uses very elementary trigonometry which is discussed here on this page, and the other uses the concept of limits which will be discussed elsewhere.

Consider a unit circle with center \( O \). Let \( \overleftrightarrow{OC} \) and \( \overleftrightarrow{OA} \) make an angle of \( x \leq 90^{\circ} \), where \( A \) and \( C \) are on the circle and \( \overleftrightarrow{OC} \) is the x-axis as shown in the left diagram below. Let \( E \) be the mid-point of \( \overline{AC} \). Let \( \varphi = \angle ACO \). From right triangle \( \bigtriangleup OCE \) we have \( \varphi = 90^{\circ} - \frac{1}{2}x \) and hence \( \sin(\varphi) = \cos\left(\frac{1}{2}x\right)\), \( \cos(\varphi) = \sin\left(\frac{1}{2}x\right) \) and \( \overline{EC} = \sin\left( \frac{1}{2}x\right) \). Therefore, \( \overline{AC}=2\overline{EC}=2\sin\left(\frac{1}{2}x\right) \). Because the radius of a unit circle is 1, from right triangle \( \bigtriangleup AOB \) we have \( \overline{OB} = \cos(x) \) and \( \overline{BC} = 1 - \cos(x) \). From right triangle \( \bigtriangleup ACB \) we have \[ \overline{BC}=\overline{AC}\cos(\varphi) =\overline{AC}\sin\left(\frac{1}{2}x\right) = 2\sin^2\left(\frac{1}{2}x \right) \] Because \( \overline{BC} = 1 - \cos(x) \), we have \[ 1 - \cos(x) = 2\sin^2\left(\frac{1}{2}x \right) \] The half (or double) angle identity gives the following: \[ 1 - \left( \cos^2\left(\frac{1}{2}x\right) - \sin^2\left(\frac{1}{2}x\right) \right) = 2\sin^2\left(\frac{1}{2}x \right) \] Simplifying yields the Pythagorean Identity.

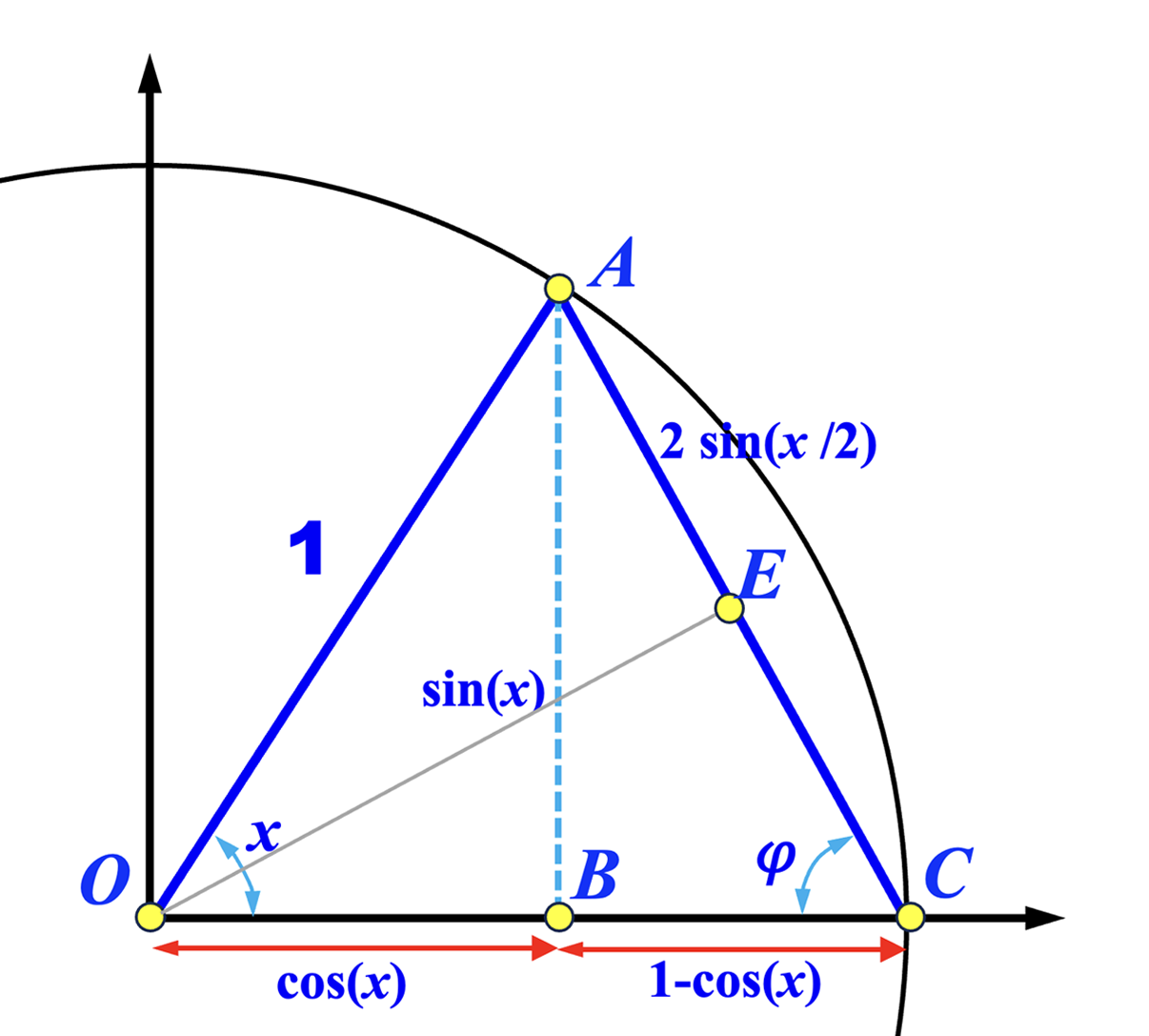
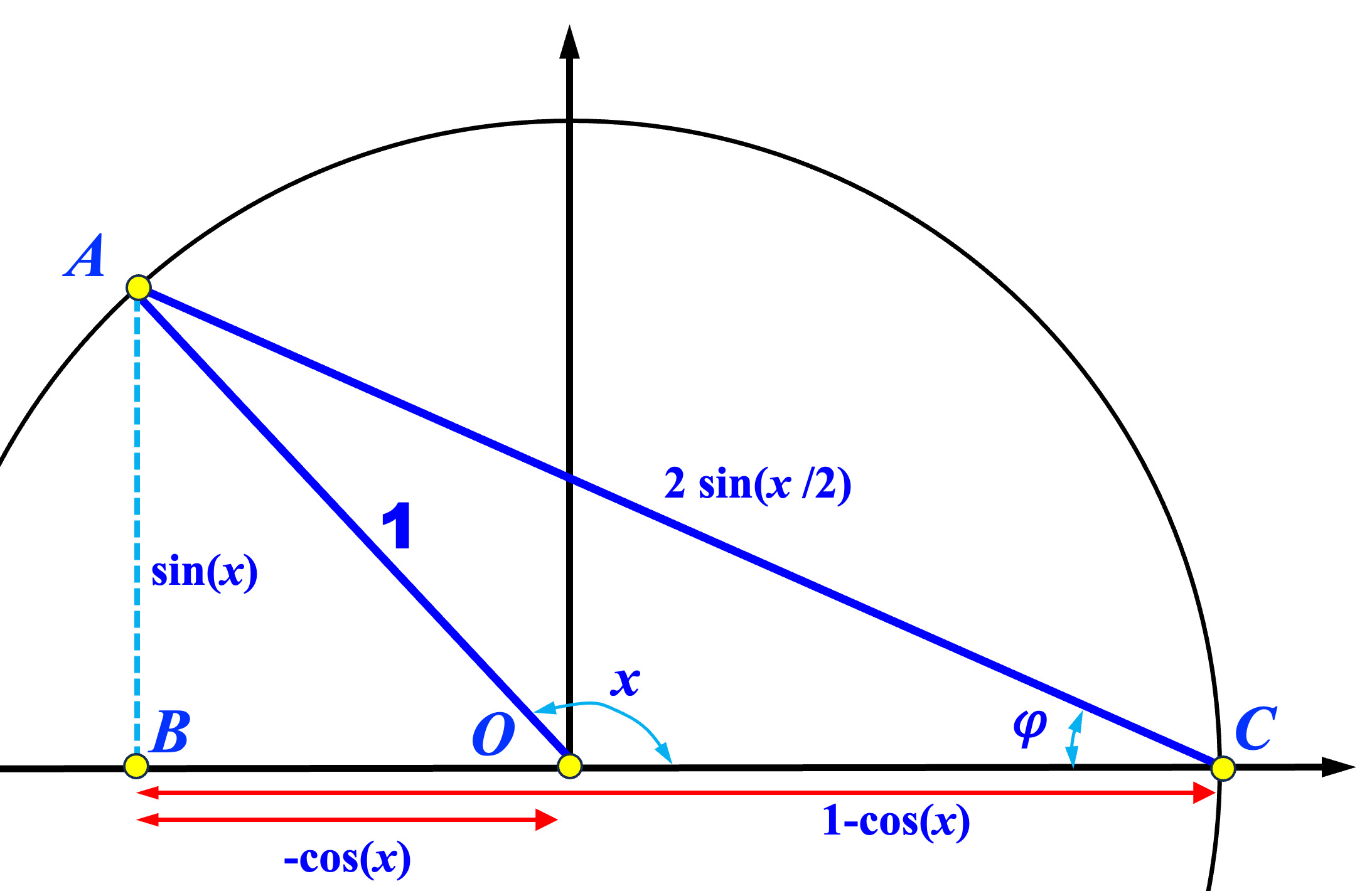
If \( x > 90^{\circ} \) as shown in the right diagram above, then \( \overline{BO} = \cos(\angle AOC) = \cos(180^{\circ}-x)= -\cos(x) \). The proof is still valid.

Finally, for any acute angle \( \theta \), using \( x = 2\theta \) in the proof yields the Pythagorean Identity for any acute angle.

Go back to Home Page.