Paul J. Maiorano's 1998 Proof

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 20, 2025

Paul J. Maiorano published in 1998 a very interesting proof of the Pythagorean Identity using coordinate geometry. You may find Maiorano's paper at jstor (pp. 620).

Given a right triangle \( \bigtriangleup ABC \) with \( \angle C = 90^{\circ} \) and \( \angle A = \theta < \angle B \), place \( A \) at the coordinate origin and \( B \) at coordinates \( (c,0) \). Please see the diagram below. Of course, \( C \) has the coordinates \( (b\cdot\cos(\theta),b\cdot\sin(\theta)) \). The euqtaion of \( \overleftrightarrow{AC} \) is \( y = \left( \frac{\sin(\theta)}{\cos(\theta)}\right)x\). The equation of \( \overleftrightarrow{BC} \) is \( y = -\left( \frac{\cos(\theta)}{\sin(\theta)}\right)(x-c)\). Note that the relationship of slopes of two perpendicular lines does not need the Pythagorean Theorem nor the Pythagorean Identity.

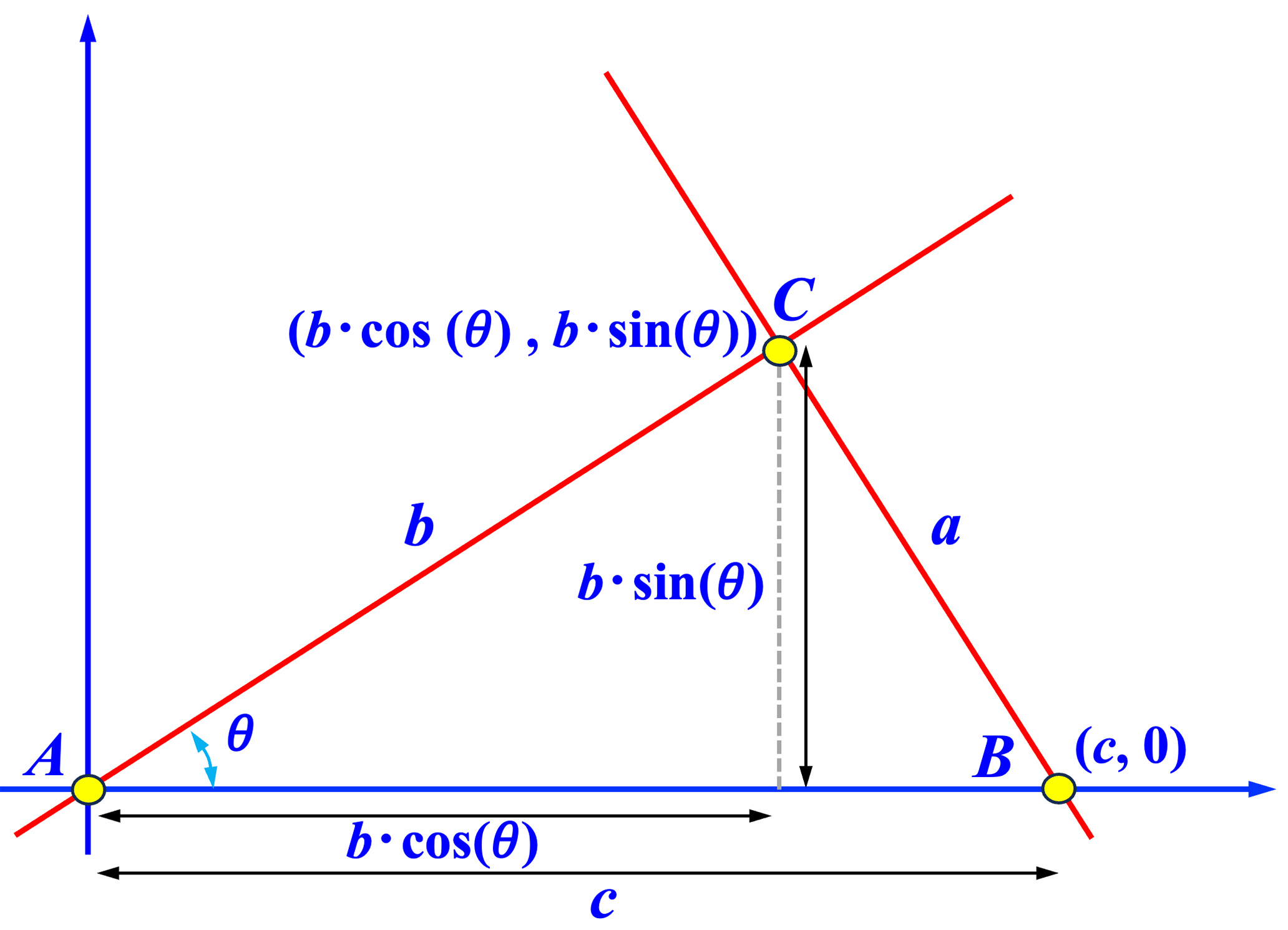
Because \( C=(b\cdot\cos(\theta),b\cdot\sin(\theta))\) is on the line \( \overleftrightarrow{BC} \), plugging \( x = b\cdot\cos(\theta) \) and \( y = b\cdot\sin(\theta) \) into the equation of \( \overleftrightarrow{BC} \) yields \[ b\cdot\sin(\theta)=-\frac{\cos(\theta)}{\sin(\theta)}(b\cdot\cos(\theta)-c). \] By noting \( b=c\cdot\cos(\theta) \) and simplyfing, we have the Pythagorean Identity easily.

Go back to Home Page.