A Simplified Version of Mike Staring's Proof

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created October 24, 2025

Staring's proof can be simplified using trigonometry. The following diagram is a simplified version of the one shown in Staring's proof. In right triangle $ \bigtriangleup ABC $, $ \angle C = 90^{\circ} $, $ a = \overline{BC} $ is a cosstant, $ x = \overline{AC} $ is a variable and the length of the hypotenuse $ f(x) = \overline{AB} $ is a function of $ x$. Let $ \theta = \angle BAC $. If $ x $ is increased by $ \Delta x $ so that $ \overline{CD} = x + \Delta x $ we have $ \overline{AD} = \Delta x $ and $ \overline{BD} = f(x+\Delta x)$. Let $ \alpha = \angle CDB $ and $ \beta = \angle ABD $, and let $ E $ be a point on $ \overline{BD} $ such that $ \overline{BE} = \overline{BA} = f(x) $. Thus, $ \overline{ED} = f(x+\Delta x) - f(x)$. In this way, we have $ \varphi = \angle AEB = 90^{\circ}-\frac{\beta}{2} $, $ \angle AED = 180^{\circ} - \varphi = 90^{\circ}+\frac{\beta}{2} $ and $ \gamma = \angle DAE = 180^{\circ}-\left( \theta + \angle BAE \right) = 180^{\circ} - (\theta+\varphi) = 180^{\circ} - \left( \theta + 90^{\circ}-\frac{\beta}{2} \right) = 90^{\circ} - \left( \theta - \frac{\beta}{2} \right)$.

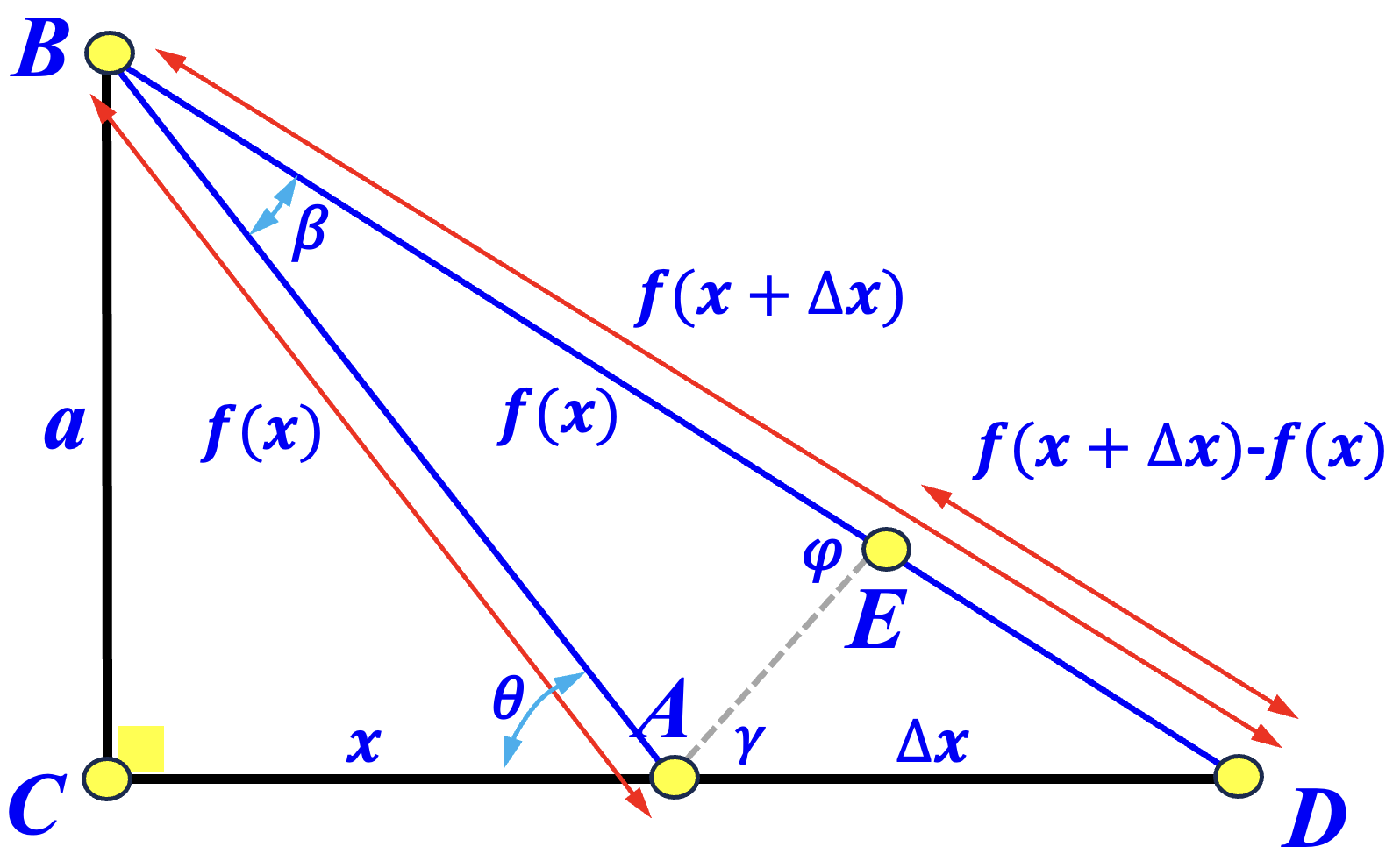
Consider $ \bigtriangleup AED $. The Law of Sines gives \[ \frac{\overline{ED}}{\sin{\gamma}} = \frac{\overline{AD}}{\sin(\angle AED)} = \frac{f(x+\Delta x)-f(x)}{\sin(\gamma)} = \frac{\Delta x}{\sin\left(90^\circ+\frac{\beta}{2}\right)} \] As a result, we have the following: $$ \begin{eqnarray*} f^{\prime}(x) &=& \lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \\ &=& \lim_{\beta \rightarrow 0} \frac{\sin(\gamma)}{\sin\left( 90^{\circ}+\frac{\beta}{2}\right)} = \lim_{\beta\rightarrow 0} \frac{\sin\left(90^{\circ} - \left( \theta - \frac{\beta}{2} \right)\right)}{\sin\left(90^\circ+\frac{\beta}{2}\right)} \\ &=& \lim_{\beta\rightarrow 0} \frac{\cos\left( \theta - \frac{\beta}{2} \right)} {\sin\left(90^\circ+\frac{\beta}{2}\right)} = \cos(\theta) = \frac{x}{f(x)} \end{eqnarray*} $$ Therefore, we have $ f(x)\cdot f^{\prime}(x) = 1$ or $ (y)dy = (x)dx $. Integrating both sides yields $ f^2(x) = y^2 = x^2 + C$, where $ C $ is a constant. Because $ f(0) = a$, we have $ f^2(x) = x^2 + a^2$ and hence the Pythagorean Theorem holds.
If $ \Delta x < 0$, then $ \overline{BD}=f(x)$ and $ \overline{BA}=f(x-\Delta x)$. The remaining of the proof is the same and will not be repeated.
Go back to Home Page.