Half-Angle Identity for Tangent

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 29, 2025

Stephen M. Robinson published a 2-page paper The Tangent of a Half-Angle in 1965. Robinson's proof is very short and nearly trivial. This proof uses only the definition of the tangent function. F. E. Wood did the same in 1949, but the angle difference identity for the sine function was used while Robinson's proof avoided this completely. Here is F. E. Wood's paper.

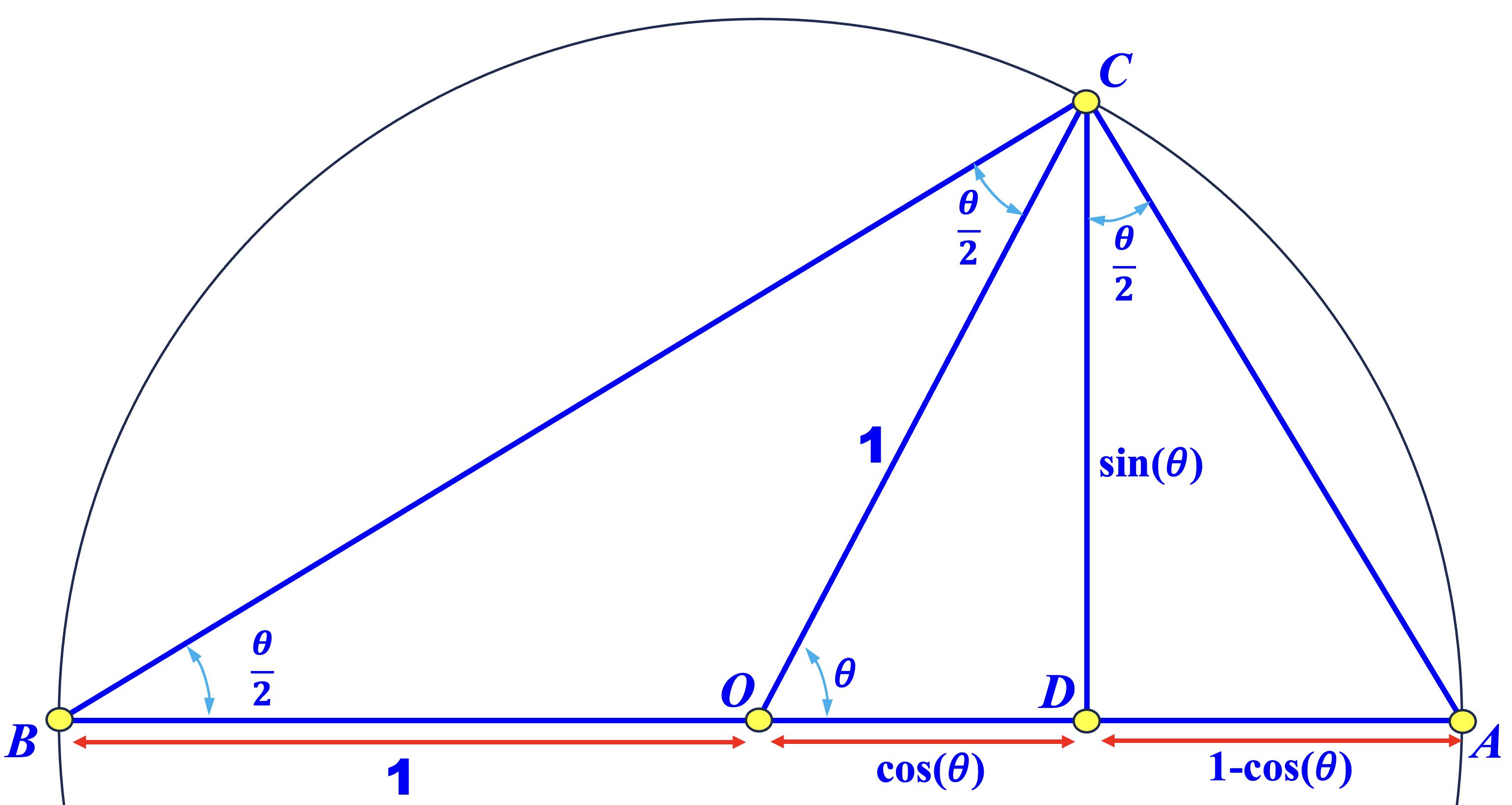
Let \( O \) be the center of a unit circle and \( \overline{AB} \) a diameter as shown below. Let \( C \) be on the circle such that \( \angle AOC = \theta \) and let \( D \) be the perpendicular foot from \( C \) to \( \overleftrightarrow{AB} \). In this way, we have \( \angle ABC = \angle BCO = \angle ACD = \frac{1}{2}\theta \). From the right triangle \( \bigtriangleup COD \), we have \( \overline{OD} = \cos(\theta) \) and \( \overline{CD} = \sin(\theta) \). From the right triangle \( \bigtriangleup BCD \), we have \[ \tan\left( \frac{\theta}{2} \right) = \frac{\overline{CD}}{\overline{BD}} = \frac{\sin(\theta)}{1+\cos(\theta)} \] From the right triangle \( \bigtriangleup ACD \), we have \[ \tan\left( \frac{\theta}{2} \right) = \frac{\overline{AD}}{\overline{CD}} = \frac{1-\cos(\theta)}{\sin(\theta)} \] Combining the above two together yields \[ \frac{\sin(\theta)}{1+\cos(\theta)} = \tan\left( \frac{\theta}{2} \right) = \frac{1-\cos(\theta)}{\sin(\theta)} \] Simplifying the above yields the Pythagorean Identity.

Go back to Home Page.