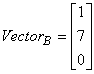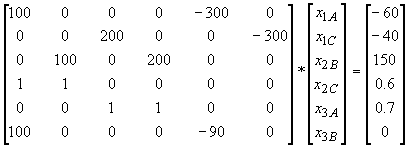MATRIX METHODS FOR SOLVING
SIMULTANEOUS EQUATIONS
(Using Microsoft Excel®)
(by Tomas Co , MTU, September 17, 2002)
Suppose we have a set of linear equations such as
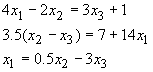 (Eqn set 1)
(Eqn set 1)
and we need to find the values of x1, x2 and x3 that would satisfy Eqn
set 1.
Procedure:
-
Set up the problem first in standard format
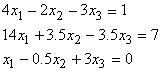 (Eqn set 2)
(Eqn set 2)
-
Translate problem to matrix form
 (Eqn 3)
(Eqn 3)
-
Solve the matrix equation
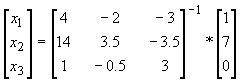 where
where
 is the matrix inverse of
is the matrix inverse of 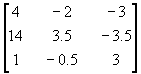
Below, we show how to perform the matrix operation by using MS Excel®.
Procedure for solving matrix equation in Excel®:
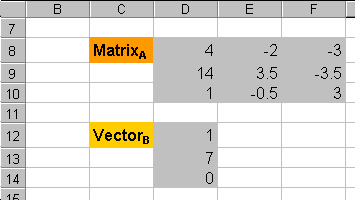
Step 1. Set up the matrices.
Let 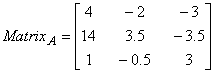 and
and 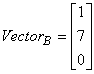
Input the values into the cells in the spreadsheet
 Remarks/Tips:
Remarks/Tips:
-
It is helpful to use a text label and a colored background to increase
the visibility of the matrices. This does not really affect the calculation.
-
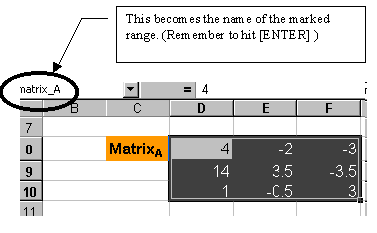
It is easier for later calculation to actually give the array a name. For
example to give the array ranging from D8 to F10 a name say "matrix_A":
-
First mark the range,
-
Then go to the box in the upper left corner and change it to matrix_A
and hit [ENTER] (If you do not hit [ENTER] the name will not be registered).
-
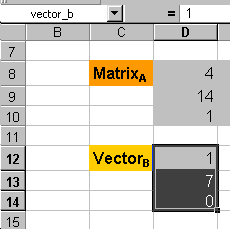
You can do the same and name the range D12:D14 and give the name: vector_b
 Step 2.
Select a range of elements for the solution, e.g. range G12:G14 below
and give the array a name, e.g. solution.
Step 2.
Select a range of elements for the solution, e.g. range G12:G14 below
and give the array a name, e.g. solution.

Step 3. Solve the matrix equation.
While the array named "solution" is selected, go to the formula box
and type-in the equation for the solution (don't hit [ENTER] yet ) :
= MMULT( MINVERSE( matrix_A ), vector_b )
Caution:
-
Remember to include the equal sign
-
Do not hit the [ENTER] key yet!!! Instead, after typing the formula, you
have to use the combination of keystroke: [CNTRL]-[SHIFT]-[ENTER]. Curly
brackets should appear to signify that you are using array operations.
Before pressing CTRL-SHIFT-ENTER:

After pressing CRTL-SHIFT-ENTER:
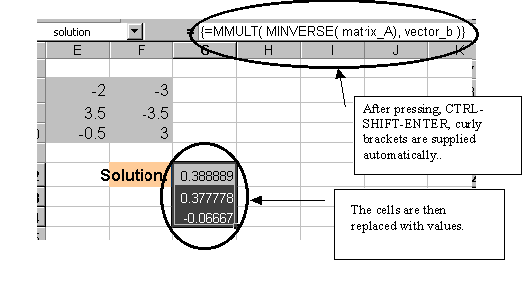
The solution to the problem is : x1 = 0.389, x2
=
0.378 and x3 = -0.0667 .
Remarks:
-
MMULT(..) is the Excel®
function for matrix multiplication.
-
MINVERSE(..) is for matrix inverse operation.
-
Remember not to put spaces between the functions and the parenthesis, i.e.
typing: MMULT (..) will give an
error. Some spaces inside the parenthesis
are allowed.
APPLICATION EXAMPLE
Problem Statement:
Stream 1 containing 30 wt% A is mixed with stream 2 containing 40 wt%
B to produce a mixture coming out as stream 3 which is composed of 50 wt%
C. 30% of component A in stream 3 comes from stream 1.
The mass ratio of stream 1 to stream 2 is 0.5 kg Strm1/kg Strm 2. Find
the compositions of all the streams at steady state.
Solution:
Basis: m1=100 kg
m2= m1/0.5 = 200 kg
m3=m1+m2=300 kg
Component Balances:
100 x1A + 200 (0.3) = 300 x3A
100 (0.4) + 200 x2B = 300 x3B
100 x1C + 200 x2C = 300 (0.5)
Sum of fractions:
x1A + 0.4 + x1C =1
0.3 + x2B + x2C = 1
Additional information:
100 x1A = 0.3 (300 x3A )
Gather all equations together into matrix form,
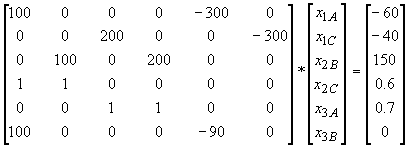 Next, implement the matrix operation through Excel®:
Next, implement the matrix operation through Excel®:
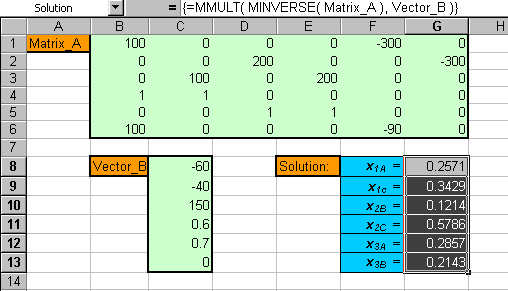
(To download a zipped copy of the Excel spreadsheet which produced
the example above,
click here )
This page was last updated 9/17/02
This page is maintained by
Dr. Tomas Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
Hougton, MI 49930
tbco@mtu.edu
Click here to return to home page
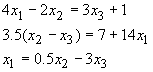 (Eqn set 1)
(Eqn set 1)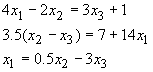 (Eqn set 1)
(Eqn set 1)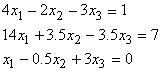 (Eqn set 2)
(Eqn set 2) (Eqn 3)
(Eqn 3)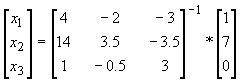
 is the matrix inverse of
is the matrix inverse of 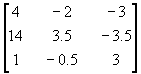
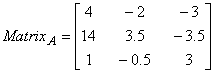 and
and