Figure 1.
I. Preliminaries:
a) Complex Mapping: Given a rational polynomial function,
G(s) = num(s)
/ den(s)
where num(s) is the numerator polynomial in s,
and den(s) is the denominator polynomial in s.
Then if s is a complex number, G(s) is also a complex number, and the value of s is said to be mapped from the s-plane to the G(s)-plane.
Ex. G(s) = 1/(1.5s+1). Let s = 1+2i, G( 1+2i ) = 1/( 1.5*(1+2i) + 1 ) = 0.1639 - 0.1967i
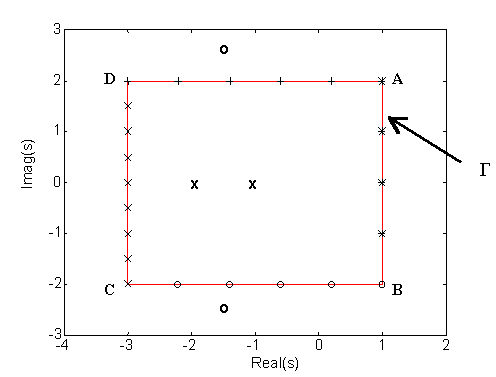
b) A simple closed path G is one which starts and ends at the same point without crossing itself.
II. Complex mapping theorem:
Given: 1) A rational polynomial function, G(s), and
2) A simple closed path G in the s-plane which does not pass through any poles or zeros of G(s).Then: As s traverses the path G in the clockwise direction, the map G(s) will encircle the origin N times in the clockwise manner, such that
where Z is the number of zeros of G(s) inside G, while P is the number of poles of G(s) inside G.
Example: G(s) = ( s2+3s+8 )/( s2+3s+2 )
zeros: -1.5 + 2.4i, -1.5 - 2.4i poles: -2, -1
G is the path A-B-C-D-A, as shown in figure below:

Since Z = 0 and P = 2, the complex mapping theorem predicts N = 0-2 clockwise encirclements, or 2 counterclockwise encirclements of the origin.To show this is true, we use the following evaluations,
|
|
|
|
|
|
A
|
1.0 + 2.0i
|
1.1154 - 0.5769i
|
|
|
1.0 + 1.0i
|
1.6000 - 0.6000i
|
|
|
|
1.0
|
2.0000
|
|
|
|
1.0 - 1.0i
|
1.6000 + 0.6000i
|
|
|
|
B
|
1.0 - 2.0i
|
1.1154 + 0.5759i
|
|
|
0.2 - 2.0i
|
0.8303 + 0.8484i
|
|
|
|
-0.6 - 2.0i
|
0.1675 + 0.8712i
|
|
|
|
-1.4 - 2.0i
|
-0.4026 + 0.1323i
|
|
|
|
-2.2 – 2.0i
|
-0.0265 – 0.7644i
|
|
|
|
C
|
-3.0 – 2.0i
|
0.7000 – 0.9000i
|
|
|
-3.0 – 1.5i
|
0.9262 – 1.3292i
|
|
|
|
-3.0 – 1.0i
|
1.6000 – 1.8000i
|
|
|
|
-3.0 – 0.5i
|
2.9765 – 1.6941i
|
|
|
|
-3.0
|
4.0000
|
|
|
|
-3.0 + 0.5i
|
2.9765 + 1.6941i
|
|
|
|
-3.0 + 1.0i
|
1.6000 + 1.8000i
|
|
|
|
-3.0 + 1.5i
|
0.9262 + 1.3292i
|
|
|
|
D
|
-3.0 + 2.0i
|
0.7000 + 0.9000i
|
|
|
-2.2 + 2.0i
|
-0.0265 + 0.7644i
|
|
|
|
-1.4 + 2.0i
|
-0.4026 – 0.1323i
|
|
|
|
-0.6 + 2.0i
|
0.1675 – 0.8712i
|
|
|
|
0.2 + 2.0i
|
0.8303 – 0.8484i
|
|
|
|
A
|
1.0 + 2.0i
|
1.1154 – 0.5769i
|
|
The plot in Figure 2 verifies that there are indeed
2 counterclockwise encirclements of the origin.
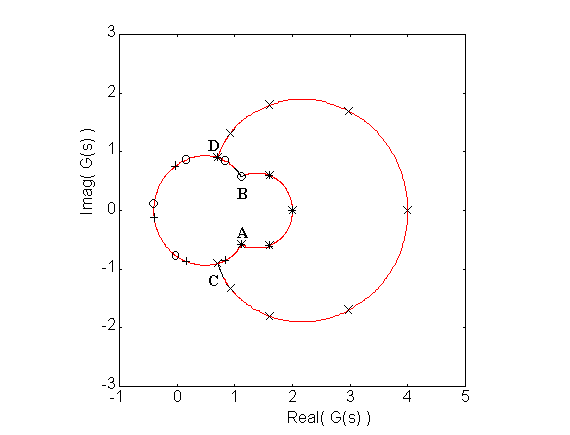
FIGURE 2.
This page is maintained by Tomas B. Co (tbco@mtu.edu).
Last revised 2/8/1999.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295