Standard Form of nth Order LODE:
where the ai’s are constant coefficients such
that an is not zero, and f(t) is the forcing function.
If f(t)=0 then equation (1) is said to be homogenous.
Solution:
The complete solution to equation (1) is a sum of two parts: the complementary
solution xc, and the particular solution xp,
The complementary part, xc (t) is the solution
to the equation when f(t) is replaced by 0, i.e. made homogenous.
It contains n arbitrary constants, which are evaluated later to
fit boundary or initial conditions.
The particular part, xp (t), is a solution which solves the original equation, i.e. when f(t) is put back into the equation. It does not have any arbitrary constant and must be linearly independent from the complementary solution.
The procedure involves the following steps:
Complementary Solution:
First, assume that the complementary solution has the form:
where s is a parameter yet to be determined. Then the kth
derivative of xc (t) is given by
Thus after substitution of (3) into (1), while setting f(t)=0,
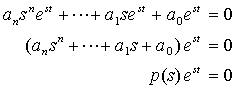 (5)
(5)
here p(s) is a polynomial function of s of degree
n
given by
Remarks:
Let the roots of p(s) be {s1, s2,
… , sn}, then the complementary solution is going to be
a sum of terms of exp(skt) multiplied by arbitrary coefficients
and/or appropriate powers of t
depending on how many times the root
is repeated.
For each real root sA that may have been repeated kA times in the set, include the following terms to the complementary solution,
![]()
where A0, …, AkA are arbitrary coefficients.
For each pair of complex roots sB= a + ib and sC = a - ib that may have been repeated kB=kC times in the set, include the following terms to the complementary solution,
![]()
where B0 , …, BkB , C0 ,
…, CkC are arbitrary coefficients.
Particular Solution (using the method of undertermined coefficients)
Depending on the form of f(t), assume a similar form for xp (t) but containing unknown coefficients. (If a term in the assumed xp (t) matches any term of xc (t), multiply these terms by t m where m is large enough to keep it independent xc (t).
These assumed terms are then substituted into the differential equation. The following steps are then implemented:
|
|
|
|
|
|
|
|
|
|
|
|
|
A t m exp( r t ) sin ( q t ) |
(E0 + E1 t + … + Em tm) exp( r t ) sin ( q t ) |
Click here for an example.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295