A Graphical Interpretation of Poles and Zeros
 
 
The poles of a rational polynomial transfer function are usually just defined as the roots of the denominator polynomial of the transfer function.  Likewise, the zeros of a transfer function are simply the roots of the numerator polynomial. However, It may be instructive to understand why the word "poles" and "zeros" have been introduced to described these critical values of a transfer function. Both these terms refer to the behavior around the specific points.
Consider the transfer function,
with s as a complex number. When one plots the magnitude of G(s), one can immediately notice the a singularity will occur around the point s=1. If a 3D plot is used to show the magnitude, one sees a post or a pole that shoots up to infinity around the singular point.
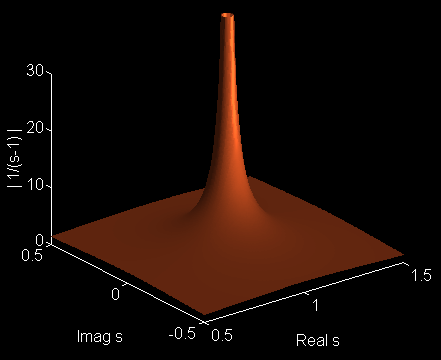
On the other hand, suppose the transfer function is given by,


H(s)=s-1

For this situation, the 3D plot of the magnitude of H(s) goes to zero around the neighborhood of s=1.


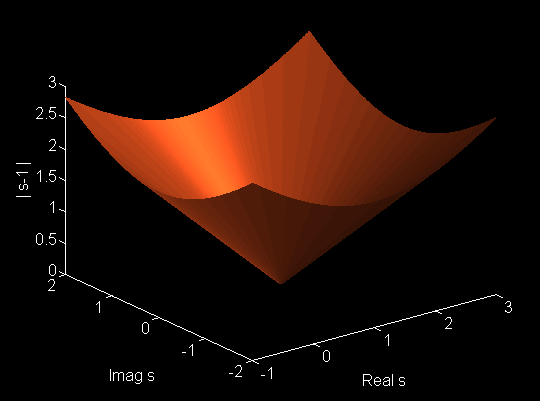
The picture of |H(s)| shows an inverted cone whose tip is located at s=1, with the value of |H(s)|=0 at that point. Note further that as domain is enlarged, the surface of |H(s)| does not flatten out but grows linearly with distance from the zero point, s=1.
 

The flatness of the surface of the magnitude of a transfer function is actually dependent on the order of the numerator polynomial and the denominator polynomial:

  • If the order of the numerator polynomial is greater than the order of the denominator polynomial the surface will not flatten as the value of s goes away from either the zeros or poles. This is referred to a physically unrealizable transfer function.
  • If the order of both numerator and denominator polynomial is the same, then the surface will flatten out to be a horizontal plane away from the zeros and poles. The height of this horizontal portion may or may not be zero. This is referred to as a proper transfer function.
  • If the order of the numerator polynomial is smaller than the order of the denominator polynomial, then it is a special case of the proper transfer function. The height of the surface will be zero as the function goes away from the zeros and/or poles.
    • For example, consider a proper transfer function given by


    There is one pole at s=-2 and a zero at s=+1. The 3D plot of the magnitude of P(s) is shown below. Notice that the surface flattens out to a height of 50 as one goes away from both points.



     

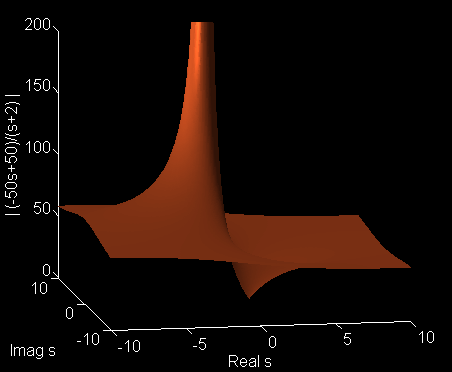
    This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 2/28/2001.

         Tomas B. Co
         Associate Professor
         Department of Chemical Engineering
         Michigan Technological University
         1400 Townsend Avenue
         Houghton, MI 49931-1295

    Back to Homepage