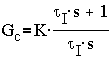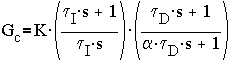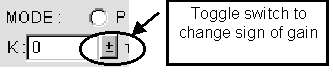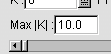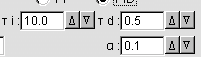Brief Manual
for PID Root Locus Generator
I. Input the coefficients of the transfer function.
( Note: throughout the program, when the values in text are being
edited, the font color will change to red. This indicates that the values
have not yet been entered. Press the [TAB] or [ENTER] keys
to accept the new values. After doing so, the font color will change back
to black.)
-
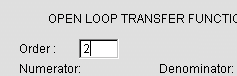
Input the order of the polynomials
-
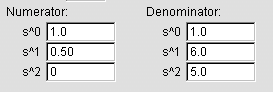
Input the coefficients in the corresponding text boxes
II. Proceed to obtain root locus by clicking
on the [PLOT ROOT LOCUS] button located at the bottom.

III. Change parameters to observe behavior of root locus
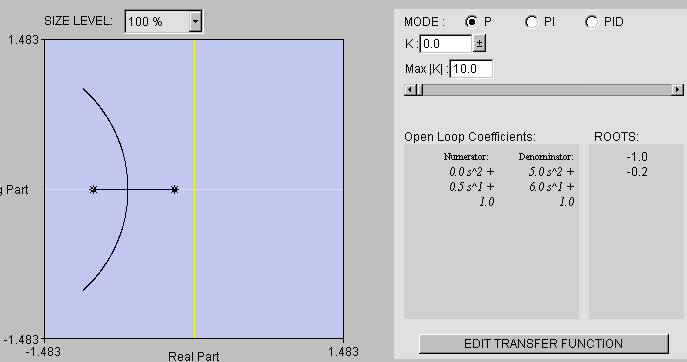
The characteristic roots should appear as star-symbols
in the plot. The values of the roots are given in the rightmost panel.
-
Select controller mode: P, PI or PID
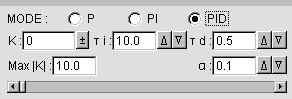
The transfer functions used for the controllers are:
Proportional Control: 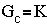
PI Control: 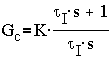
PID Control: 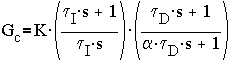
-
Choose whether gain is positive or negative.
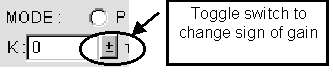
A label should appear below the scrollbar to indicate
that the negative domain was chosen.
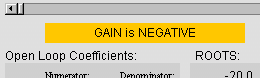
-
Enter a different maximum absolute gain if needed by entering
positive values in the textbox above the scrollbar.
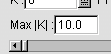
-
Slide the scrollbar to change the gain values within the
range chosen.

Alternatively, key in specific values for gain
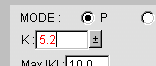
( Note again the value of 5.2 in the figure above is not accepted
until the user hits the [TAB] or [ENTER] keys )
-
Change parameters via up/down buttons or key-in new values
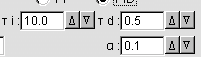
(Using the up/down buttons, the increments for tI
is
1.0,
while the increments
for tD is
0.1,
and the increments
for a is 0.01.)
-
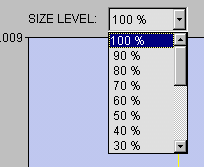
Zoom to desired levels if needed using the drop-down choice
list located above the plot.
-
Roots are color coded: Black=roots are stable and appear
in the plot. Gray=roots are stable but do not appear in plot (e.g. after
zooming in). Red=roots are unstable.
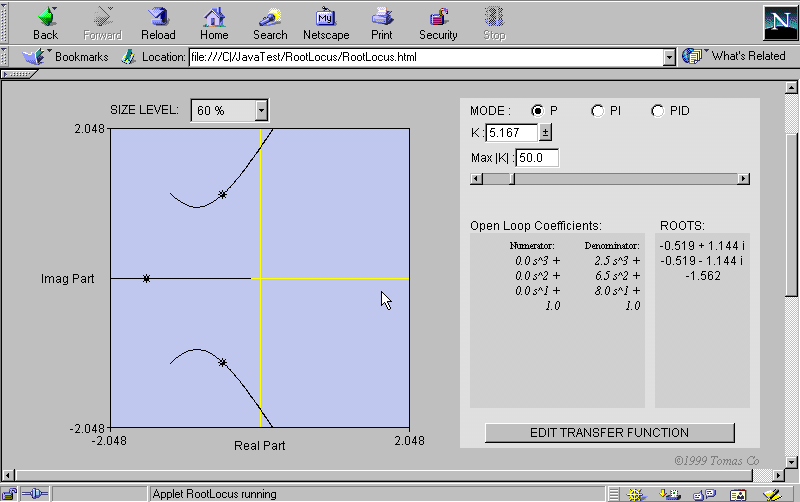
Example 1: all roots are stable and appear in plot
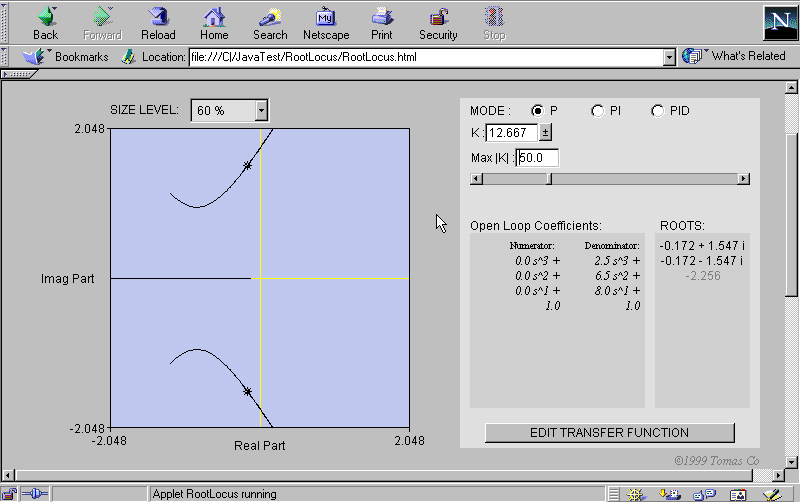
 Example 2: Three stable roots but the root at –2.256 is not
visible in the plot
Example 2: Three stable roots but the root at –2.256 is not
visible in the plot
 Example 3: Two unstable roots and one stable root (but not
in the plot)
Example 3: Two unstable roots and one stable root (but not
in the plot)
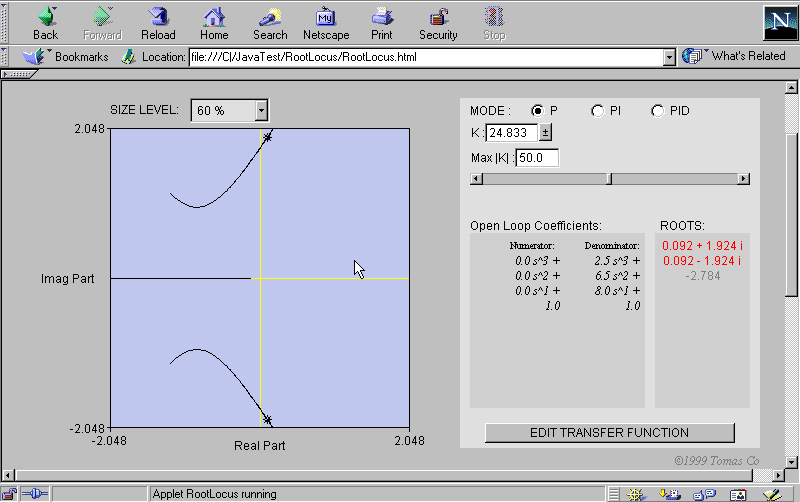
IV. Edit transfer function if needed by clicking
on [EDIT TRANSFER FUNCTION] button located at the bottom of the right panel.

This page is maintained by Tomas B. Co (
tbco@mtu.edu ). Last revised 11/30/1999.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295
Back to Homepage