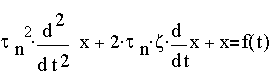
Standard Form:
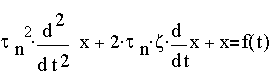
Further, consider the case where
Then the characteristic equation is :
![]()
whose roots are given by:
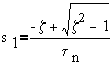
and
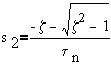
Case 1:Both roots are real and negative ( and thus stable)
Using initial condtions,
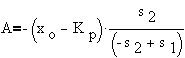
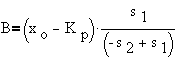
or
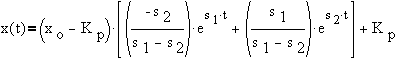
Case 2:Repeated real roots
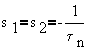
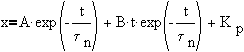
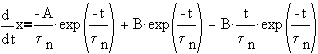
Using initial conditions,
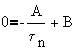
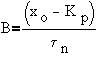
or
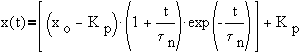
Case 3:Roots are complex conjugates
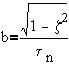
Thus,
Using initial conditions,
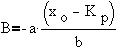
Alternatively, we can use the sin of sums formula,
comparing right hand side with,
then
from which,
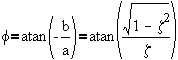
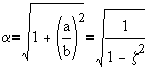
so, an alternative form for x(t) is given by
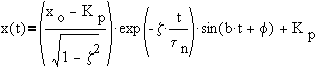
where,is the frequency
andis the phase shift
Case 4: z=0 Pure imaginary roots
Derivation
of Overshoot, Decay Ratio and Frequency (Underdamped Systems) :
a) Overshoot:
First, calculate the time when the peaks occur. To do so, obtain dx/dt, and then find the value of t which makes it zero.
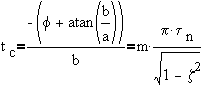
for upper peaks, The overshoot occurs at the first upper peak, i.e.
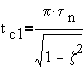
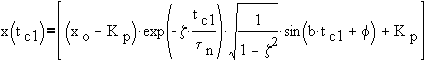
but,
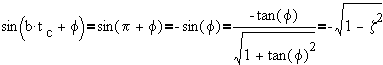
b) Decay ratioso the overshoot is given by
Compare the value at the first peak and the second upper peak. The second upper peak occurs at tc3
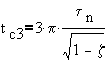
thus, the decay ratio is given by,
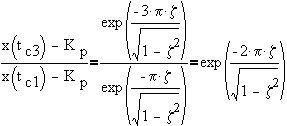
c) Frequency
The period of oscillation is the amount of time between two upper peaks
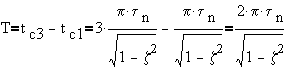
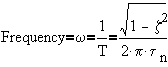
(in cycles per second or Hz)
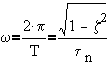
(in rads per second)
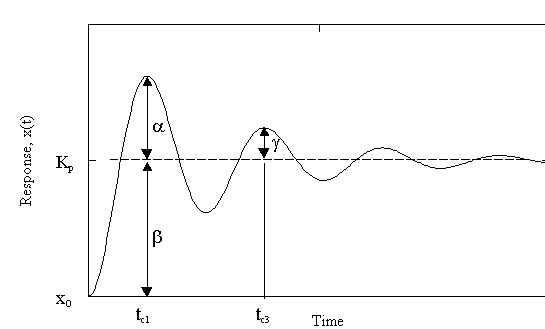
Overshoot =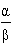
Decay Ratio=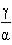
Frequency=( in rads/sec )
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 12/2//99.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295