I. Some preliminaries on complex numbers.
1. Polar forms of complex numbers:
Let
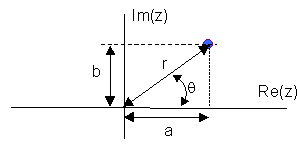
then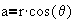
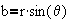
where r is known as the magnitude of z, denoted |z|, and q is known as the argument of z, denoted arg(z)
Thus the polar form for z is given bywhere,
2. Some properties of complex numbers:
Let conj(z) be the conjugate of z, e.g. conj(a+ i b)=a - i b
a)
b)
3. Functions of complex numbers yield complex numbers
4. A function of the conjugate is the conjugate of the function
Example: Let
then
Example: Let
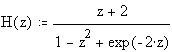
then
II. Frequency Response of a stable Transfer Function
Suppose we are given a transfer function G(s) from u(s) to y(s), whose poles all have negative real parts. Using a sinusoidal input, u(t)=A sin(wt), the Laplace transform is given by
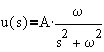
The output, y(s) in the Laplace domain is given by
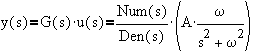
For discussion purposes, we will use a second order process (with b,c>0)
then
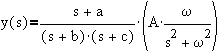
After separation into partial fractions,
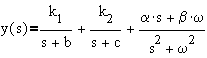
Using the short cut method to determine a and b,
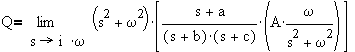
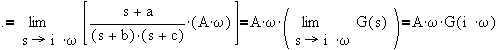
![]()
which yields
![]()
![]()
Thus,
As t goes large, the transients die out - leaving only the last two terms,
[Equation 1]:
Based on earlier discussions, this was put in the form,
[Equation 2]:
Comparing equation 1 with equation 2,
After some more rearrangements,
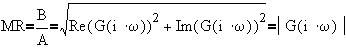
![]()