1. Preliminaries:

1. Given: G(s), a transfer function in Laplace domain
2. Required: Frequency response plots corresponding to G(s)

1. Bode Plots.

• These consist of two plots. The first plot is a plot of log modulus (in decibels) versus frequency. The second plot is the phase shift (in degrees) versus frequency. Both plots usually have the frequency in logarithmic scale.

• Using the given transfer function G(s),

2. Nyquist Plots.

• The Nyquist plots is obtained by simply plotting Imaginary(G(iw)) versus Real(G(iw))

2. Spreadsheet Implementation:

For discussion purposes, consider a second order transfer function,

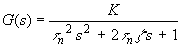
1. Set up some cells for the various parameters in the transfer function.







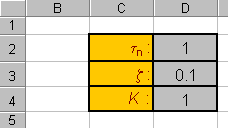
2. Next, determine the range of frequencies that are of interest. For example, let 10^-1 < w < 10¹. Since the frequency will be plotted in logarithmic scale, you can use a column to include numbers ranging linearly from -1 to 1, e.g. -1, -0.99,…, 0.98, 0.99, 1. Then use another column to evaluate the frequency, e.g. w = 10^-1, 10^-0.99, …, 10^0.98 10^0.99, 10¹.







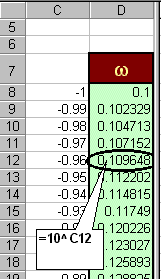
3. In the next column, build cells containing complex numbers, s=iw. This can be done by using the

COMPLEX( , ) function provided in Excel.




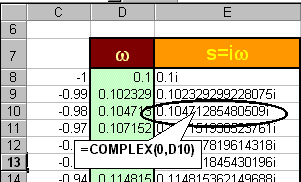
(Note: you may need to change the width of the column in order to see the numbers)
4. Now evaluate the transfer function, G(s), with s=iw, using the built-in functions, IMDIV(a,b), IMSUM(a,b), IMPRODUCT(a,b), IMPOWER(a,n) to perform complex division, sum, product and power operations on complex numbers a and b, with n as integer.







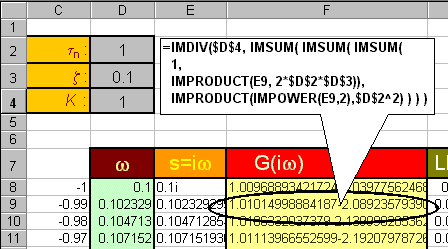
5. From the results in G(iw), obtain the Log Modulus and Phase Shift columns:







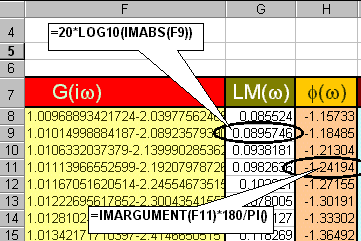
6. Also, from G(iw), obtain columns that evaluate Re[G] and Im[G], respectively:







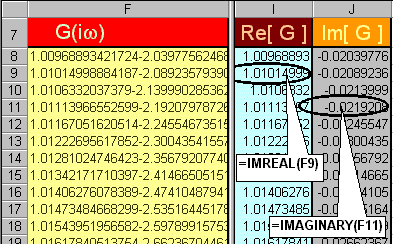
7. Using the Log modulus, Phase Shift and Frequency columns, obtains the Bode plots:






 
 
 
 
 

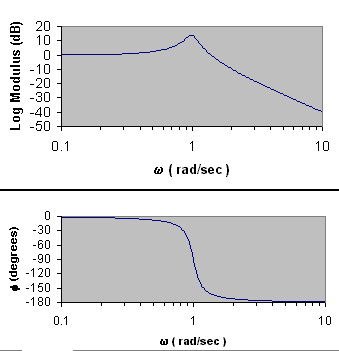
8. Using the columns for Re[G] and Im[G], obtain the Nyquist Plot:

This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 2/1/00.

          Tomas B. Co
          Associate Professor
          Department of Chemical Engineering
          Michigan Technological University
          1400 Townsend Avenue
          Houghton, MI 49931-1295

Back to Homepage