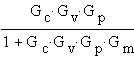I. Setup and Assumptions:

Feedback System:



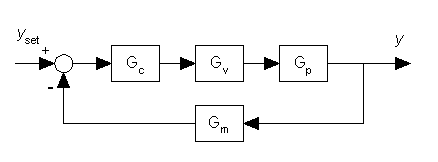
Figure 1.





Closed Loop Transfer Function:



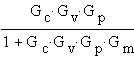
Characteristic Equation:         1 + G_cG_vG_pG_m=0

(Note: This equation is not a polynomial but a ratio of polynomials)
 

Stability Condition: None of the zeros of ( 1 + G_cG_vG_pG_m )are in the right half plane.

Assumption: G_c, G_v, G_p and G_m are all stable, i.e. stable (open-loop) process, controller, actuator and sensor. This means (1 + G_cG_vG_pG_m ) has no poles in the right half plane.
 
 

III. Preliminaries:
 

a) A transfer function G(s) is said to be proper if

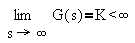
    and strictly proper if






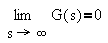
(Note: All physically realizable systems are either proper or strictly proper.)
b) If G(s) is a ratio of polynomial functions, then

• G(s) is proper if the order of the numerator polynomial is less than or equal than the order of the denominator polynomial
• G(s) is strictly proper if the order of the numerator polynomial is less than the order of the denominator polynomial

c) Nyquist path:
 
In the s-plane, the clockwise path A-B-C-A is a simple closed semi-circle contour in the right half of the complex plane as shown below:




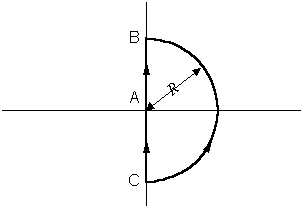
Figure 2.

As R approaches infinity, the contour will encompass all the points in the right half plane.


d) Complex mapping using the Nyquist path:
 

Let G(s) be proper, then
-  The mapping of G(s) along the path A-B is just G(iw) for w=0 to R. This information is obtained from frequency response experiments.
-  The mapping of G(s) along the path B-C is just a finite constant as R approaches infinity.
-  The mapping of G(s) along the path C-A is G(-iw) with w= - R to 0, i.e. the mirror image of G(iw).

Assume G_c, G_v, G_p and G_m are all stable. If the Nyquist plot of G_cG_vG_pG_m (s) does not encircle the point -1+0i  in the complex plane in the clockwise direction, then the system is asymptotically stable.
Proof: According to the complex mapping theorem, the map of (1+G_cG_vG_pG_m) along the Nyquist path will encircle the origin N times, where N=Z-P. Since G_c, G_v, G_p and G_m are all stable, P=0. Thus N=Z. This means the number of encirclements of the origin indicates the number of roots of the characteristic equation in the right half plane.

Thus for stability, we must have N=Z=0.

Finally, the map of G_cG_vG_pG_m (s) is the map of 1+ G_cG_vG_pG_m (s) shifted one unit to the left.
 

This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 2/9/1999.
     Tomas B. Co
     Associate Professor
     Department of Chemical Engineering
     Michigan Technological University
     1400 Townsend Avenue
     Houghton, MI 49931-1295

Back to Homepage