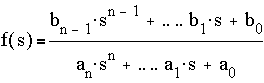
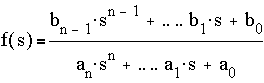
solve for the roots of ansn+…+a1s+a0=0 say: -r1, -r2, … , -rn then
![]()
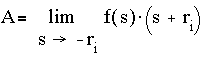
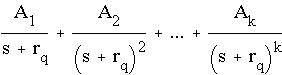
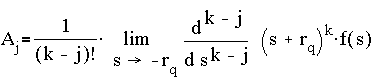
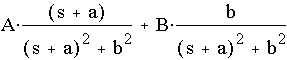
where
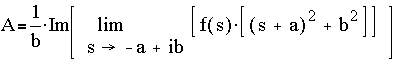
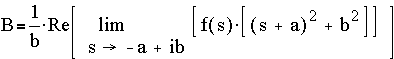
To top of page
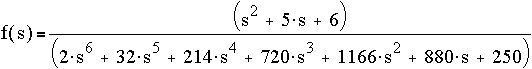
The roots of
are: -5, -4+3i, -4-3i, -1, -1, -1
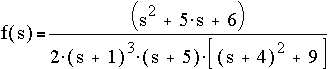
Converting to partial fractions,
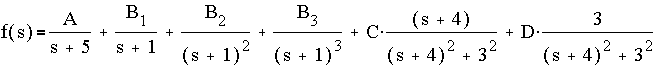
where
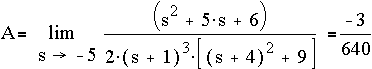
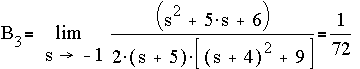
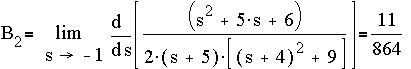
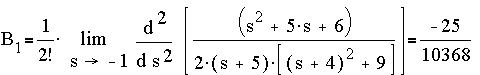
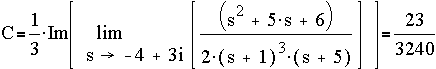
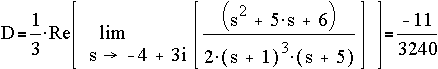
Thus the inverse Laplace transform of f(s) is
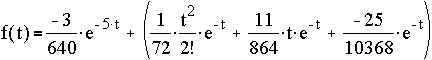
+
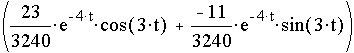
To top of page
A Sketch
of the Derivation of the Short Cut Formulas for Obtaining Coefficients
in the Partial Fractions
Case 1. (For each real and distinct root).
Suppose (-r) is an unrepeated root in the denominator, and g(s) is obtained by lumping all terms except for 1/(s+r), i.e.
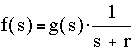 =
= ![]() + [other terms]
+ [other terms]
After multiplying both sides by (s+r),
and letting s be equal to -r, only A remains on the right hand side of the equation, so
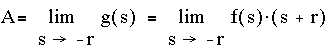
Case 2. (For each root that is repeated k times).
Suppose (-r) is a root in the denominator that is repeated k times, and g(s) is obtained by lumping all terms except for 1/(s+r)k, i.e.
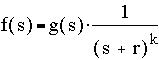
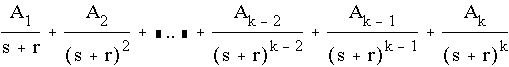
+ [other terms]
After multiplying both sides by (s+r)k,
+ [other terms](s+r)k
Take the derivative of both sides with respect to s,
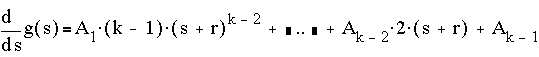
+ [other terms]k(s+r)k-1 + (s+r)k (d/ds)[other terms]
and for the second derivative,
+ [other terms]k(k-1)(s+r)k-2 + (s+r)k(d2/ds2) [other terms]
+ 2((d/ds) [other terms] )k(s+r)k-1
In general, we get for the ith derivative with respect to s,
so by choosing s = - r at the appropriate ith derivative, we have
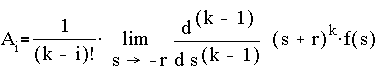
Case 3. (For each two roots that are complex conjugate pairs).
Suppose (-a+ib) and (-a-ib) are complex conjugate roots in the denominator, and g(s) is obtained by lumping all terms except for 1/[ (s+a)2 + b2 ], i.e.
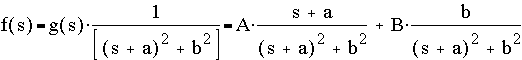
+ [other terms]
Multiplying both sides by,
![]() + [other terms][ (s+a)2+b2 ]
+ [other terms][ (s+a)2+b2 ]
By letting Q be g(s= -a+ib), the other terms disappear, leaving only A and B on the right hand side,
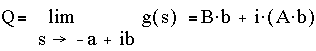
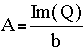
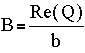
To top of page
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 1/12/2000.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295