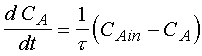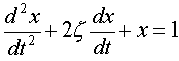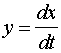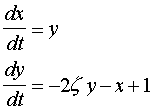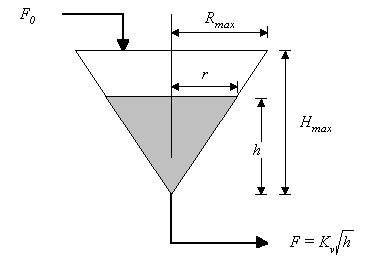
Figure 1. Conical Tank System.
Due Dec. 10, 1999

Figure 1. Conical Tank System.
Hmax = 10 ft
Kv =1 ft1/2/ s
h(0) = 2 ft
Fo =2 ft3/s
Changes in Variable Effect on Steady State Effect on Rate of Response As x increases :
Increases :
Faster :
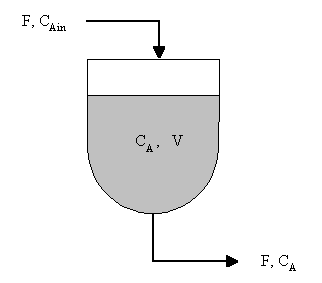
Figure 2. Storage Tank at Constant Volume