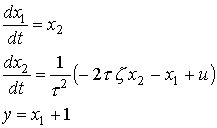 (1)
(1)I. Frequency Response Experiment.
Use the simulation located at the URL: http://www.chem.mtu.edu/~tbco/cm416/freq.html .
( Just for your information, the process inside the simulation is given by
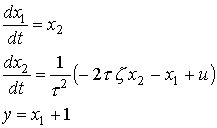 (1)
(1)with t=3.33 and z=0.2 )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I suggest at least using the following frequency values: 0.1, 0.2, 0.25,
0.27,0.28,0.29,0.3,0.32,0.4,0.5. Also use at least a value of 0.5 for amplitude
A.
II. Bode and Nyquist Plots for
Transfer Functions
Using an Excel spreadsheet (or other programs, e.g. MathCad, MATLAB,
etc.), generate the Bode Plots and Nyquist Plots for the transfer function:
![]()
for the following cases:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For a tutorial on the use of Excel for generating the plots, you can link to http://www.chem.mtu.edu/~tbco/cm416/freqexcel.html . For the use of MathCAD, a sample printout of a worksheet can be downloaded in PDF format or Postscript format.
From the Bode plots (both LM vs frequency and Phase Shift vs frequency) obtained, supply the following observations:
|
|
|
|
|
|
|
Ax=-0.5,Ay=0.5, Bx=0.5,By=-0.5 |
|
|
|
|
except Ax= -1.5 |
|
|
|
|
Ax=0.1, Ay=0, Bx=0.1, By=0.6 |
|
|
|
|
Ax= -0.8, Ay= -0.05, Bx= -1.0, By=-0.05 |
|
|