![]()
Objective:
Given a polynomial equation in s,
![]()
Without having to actually having to solve for the roots, the Routh-Hurwitz
method can be used to determine how many roots will have positive real
parts. Hence, if the polynomial equation is the characteristic equation,
this method can be used to determine the stability of the process.
Procedure:
Step 1: Build the Routh array.
(a) For rows 1 and 2, build h columns, where h = Largest integer [ (n+1)/2 ],
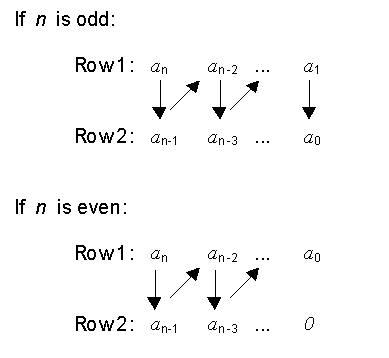
(b) For row 3 to row n+1,
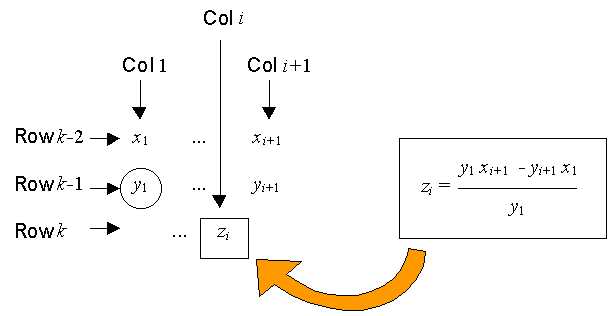
( Note: for entries in the rightmost column, column h, set x( h+1 ) = 0 and y( h+1 ) = 0 for the formulation above. )
Step 2: Extract the first column of the array and
count the number of sign changes. The number of sign changes gives
the number of roots of the polynomial which have positive real parts.
Example 1:
![]()
Then the Routh-Hurwitz array is given by
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
There are 3 sign changes in the first column, thus the conclusion is
that there are three roots that have positive real parts. ( The roots can
be obtained using root finders to be: -1.453, -0.961 + 0.93 i ,
-0.961 - 0.93 i , 0.363 + 0.678 i , 0.363 - 0.678 i ,
0.650 ).
Example 2:
![]()
The Routh-Hurwitz array is given by
|
|
|
|
|
|
|
|
|
Looking at the first column, the polynomial will have "stable" roots
(roots having only negative real parts) we need
-80 < Kc < 4.
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 1/19/1999.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295