- First Order System
- Second Order System
- Standard Form: t (dx/dt )
+ x = f(t)
- Characteristics: t = time
constant
- If f(t) = Kp = constant,
- x( t ) = Kp - [ Kp-x(0) ] exp( -t/t
)
- [ x( t ) - x(0) ] = 0.632 [ Kp
- x(0) ]
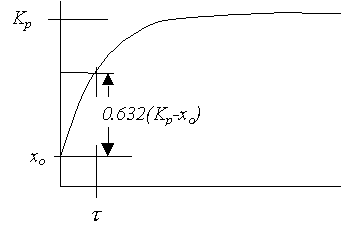
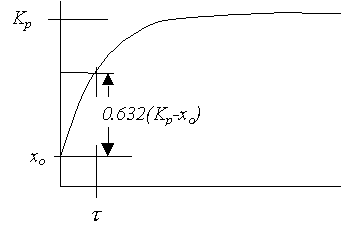
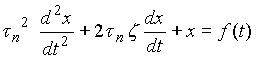
Eigenvalues:
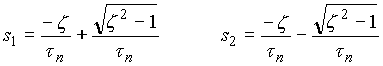
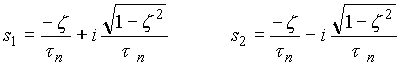
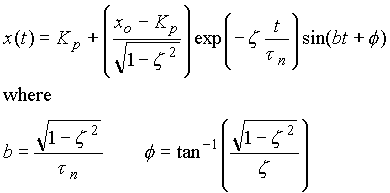
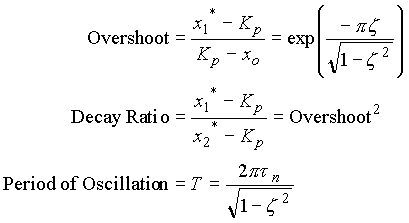
From the characteristic equation of a second order system,
the process is stable if and only if all the coefficients have the same sign.
|
|
|
|
|
|
|
|
|
|
|
|
u = ubias +kc [e
|
|
|
|
|
|
|
|
Where e = error = xset - x , kc = controller gain , tI = integral time , tD = derivative time