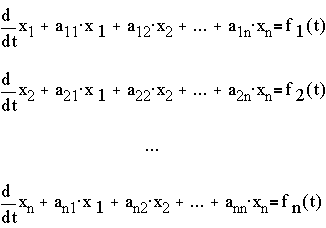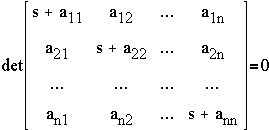Procedure:Given:(1)
1. Linearization:
Objective:
To provide a linear approximation of a process model that could predict local behavior around a chosen operating condition.
Procedure:Given:(1)
To obtain a linearized model of equation (1) with respect to the point: xo, uo and do, first obtain the following constants:
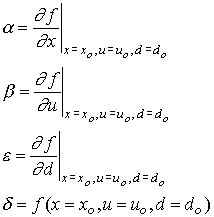
then the linearized model is given by
2. Linear Ordinary Differential Equations with constant coefficients.
- General Form:
(2)
- Solution:
where xc is the complementary solution and xp is the particular solution.
- In solving for the complementary solution, the procedure involves obtaining the characteristic equation:
(3)
whose n roots are the eigenvalues of the system described by (2).
- The eigenvalues determine the inherent behavior of the system: