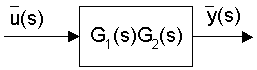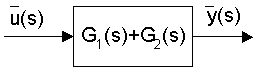- Method of Partial Fractions to find inverse Laplace transform
- Transfer Functions
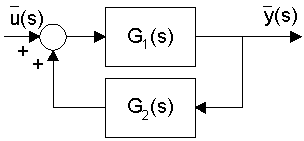
- Equivalent Transfer Functions
Given: f(s) = num(s)/den(s)
where num(s)=numerator polynomial in s, den(s)=denominator polynomial
in s
Step 1: Find the roots of the denominator polynomial, say - r1, ... , -rN
Step 2: Based on these roots separate num(s)/den(s) into partial
fractions.
Case 1: For each root, say -q, appearing k times, add
the following k terms:
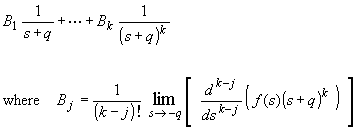
Case 2: For each complex pair of roots, say -a+ib
and -a-ib, add two
terms:
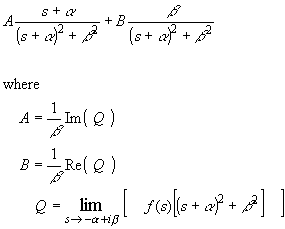
Step 3. If needed, take the inverse Laplace transforms of each
terms using the following formulas:
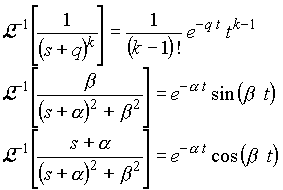
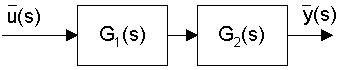
Definition: a relationship from the input variable, say u, to an output variable, say y, in the Laplace domain
Function Form: L(y) = G(s) L(u), where G(s) is the transfer function
Block Diagram Form: