Objective:
Given f(x), we want a power series expansion of this function with respect to a chosen point xo, as follows:
Method:
The general idea will be to process both sides of this equation and choose values of x so that only one unknown appears each time.
To obtain ao: Choose x=xo in equation (1). This results in
To obtain a1: First take the derivative of equation
(1)
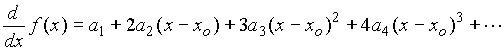 (2)
(2)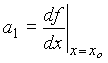
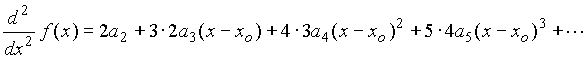 (3)
(3)
Now choose x=xo.
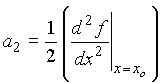
To obtain a3: First take the derivative of equation (3)
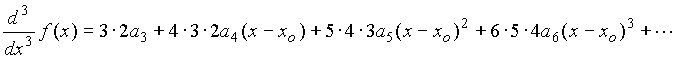 (4)
(4)
Now choose x=xo.
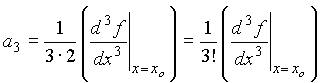
To obtain ak: First take the kth derivative of equation (1) and then choose x=xo.
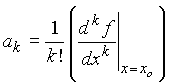
Summary:
The taylor series expansion of f(x) with respect to xo is given by:
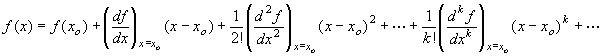
Generalization to multivariable function:
Let x, y and z be the three independent variables,
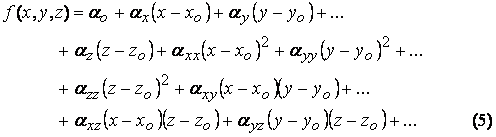

For the general case of n independent variables,
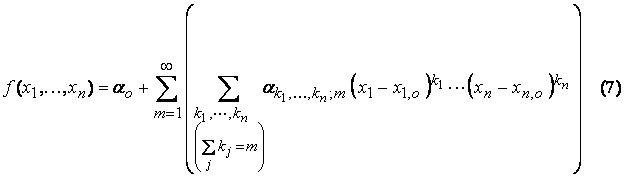
where the coefficients are given by,

(Note: the procedure above does not guarantee that the infinite series converges. Please see Jenson and Jeffreys, Mathematical Methods in Chemical Engineering, Academic Press, 1977, for a thorough discussion on how to analyze the convergence of the resulting series.)
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 06/10/2007.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295