1.4 Homework
MA 2321, Fall '03, T. Olson
- 2.
- If defined, compute the product shown using
(i) the definition (linear combinations of columns) and
(ii) the rule for computing
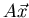 .
If the product is undefined, say why.
.
If the product is undefined, say why.
- 4.
- If defined, compute the product shown using
(i) the definition (linear combinations of columns) and
(ii) the rule for computing
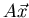 .
If the product is undefined, say why.
.
If the product is undefined, say why.
- 8.
- Write the system in the form
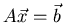 .
.
- 19.
- Let
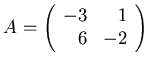 and
and
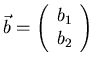 .
Show that the equation
.
Show that the equation
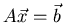 is not consistent
for all possible
is not consistent
for all possible 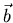 ,
and describe the set of all
,
and describe the set of all 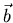 for which
for which
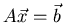 is consistent.
is consistent.
- 31.
- It can be shown that
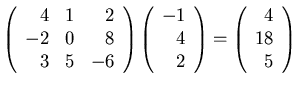 .
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
.
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
- 32.
- Let
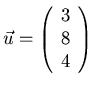 ,
,
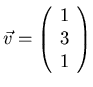 ,
and
,
and
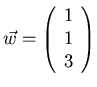 .
It can be shown that
.
It can be shown that
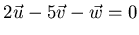 .
Use this fact (and no row operations) to solve the equation
.
Use this fact (and no row operations) to solve the equation
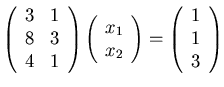 .
.
- 35.
- Let A be a
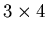 matrix, let
matrix, let 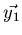 and
and
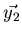 be vectors in
be vectors in
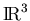 ,
and let
,
and let
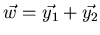 .
Suppose that
.
Suppose that
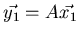 and
and
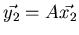 for some vectors
for some vectors 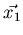 and
and
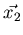 in
in
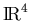 .
What fact allows you to
conclude that the system
.
What fact allows you to
conclude that the system
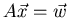 is consistent?
(Note,
is consistent?
(Note, 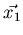 and
and 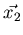 denote vectors, not
scalar entries in vectors.)
denote vectors, not
scalar entries in vectors.)
- 36.
- Let A be a
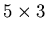 matrix, and let
matrix, and let 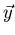 be a vector in
be a vector in
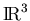 and
and 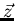 a vector in
a vector in
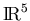 .
Suppose that
.
Suppose that
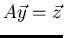 .
What fact allows you to conclude that the system
.
What fact allows you to conclude that the system
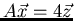 is consistent?
is consistent?
About this document ...
Tamara Olson
trolson@mtu.edu
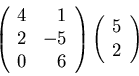
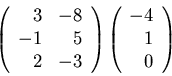
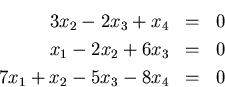
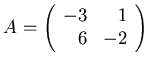 and
and
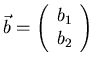 .
Show that the equation
.
Show that the equation
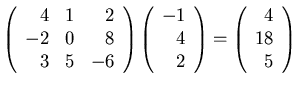 .
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
.
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
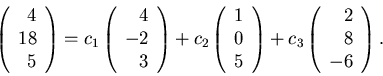
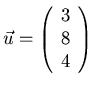 ,
,
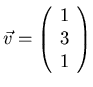 ,
and
,
and
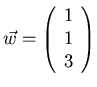 .
It can be shown that
.
It can be shown that
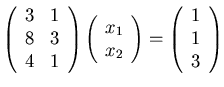 .
.
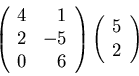
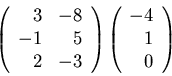
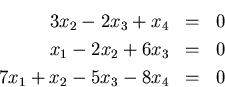
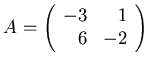 and
and
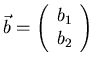 .
Show that the equation
.
Show that the equation
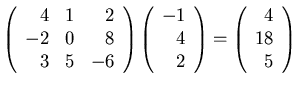 .
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
.
Use this fact (and no row operations) to find scalars
c1, c2, and c3, such that
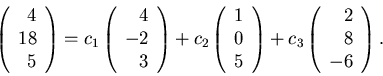
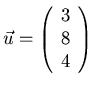 ,
,
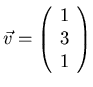 ,
and
,
and
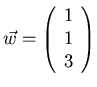 .
It can be shown that
.
It can be shown that
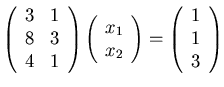 .
.