Notice that A2=I when
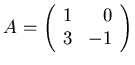 .
Use partitioned matrices to show that M2=I when
.
Use partitioned matrices to show that M2=I when
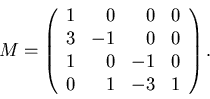
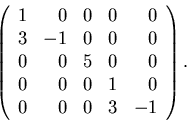
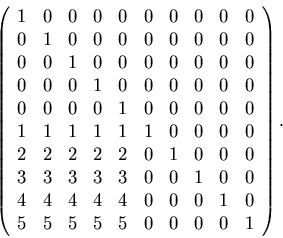
(Hint:
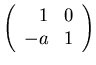 is the inverse of
is the inverse of
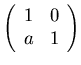 .)
.)
For each of the following problems, be sure to indicate precisely HOW you partition the matrices and how this partition is used to find your answer.
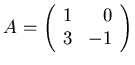 .
Use partitioned matrices to show that M2=I when
.
Use partitioned matrices to show that M2=I when
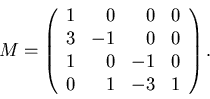
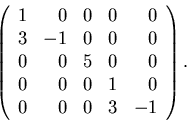
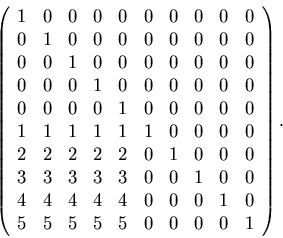
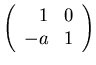 is the inverse of
is the inverse of
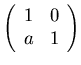 .)
.)