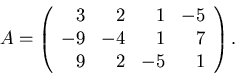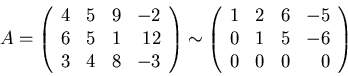2.8 Homework
MA 2321, Fall '03, T. Olson
- 7.
- Let
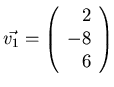 ,
,
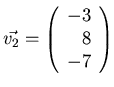 ,
,
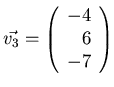 ,
,
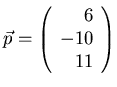 ,
and
,
and
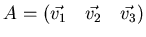 .
.
- a.
- How many vectors are in the set
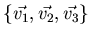 ?
?
- b.
- How many vectors are in Col A?
- c.
- Is
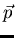 in Col A? Why or why not?
in Col A? Why or why not?
- 11.
- Give integers p and q such that Nul A is a subspace of
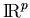 and Col A is a subspace of
and Col A is a subspace of
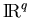 for the matrix
for the matrix
- 13.
- For A as in Exercise 11, find a nonzero vector
in Nul A and a nonzero vector in Col A.
- 23.
- The following displays a matrix A and
an echelon form of A.
Find a basis for Col A and a basis for Nul A.
- 27.
- Construct a
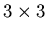 matrix A and a
nonzero vector
matrix A and a
nonzero vector
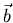 such that
such that 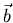 is in Col A, but
is in Col A, but 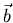 is not the same as any one of the columns of A.
is not the same as any one of the columns of A.
- 28.
- Construct a
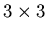 matrix A and a vector
matrix A and a vector
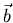 such that
such that 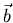 is not in Col A.
is not in Col A.
- 29.
- Construct a nonzero
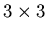 matrix A and a nonzero vector
matrix A and a nonzero vector
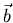 such that
such that 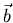 is in Nul A.
is in Nul A.
- 33.
- If Q is a
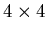 matrix and Col Q
matrix and Col Q
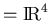 ,
what can you say about solutions of equations of the form
,
what can you say about solutions of equations of the form
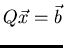 for
for 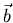 in
in
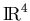 ?
?
- 35.
- What can you say about Nul B when B is a
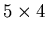 matrix with linearly independent columns?
matrix with linearly independent columns?



Next: About this document ...
Tamara R. Olson
2003-09-13
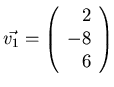 ,
,
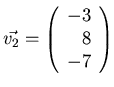 ,
,
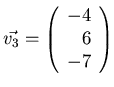 ,
,
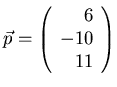 ,
and
,
and
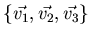 ?
?
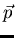 in Col A? Why or why not?
in Col A? Why or why not?
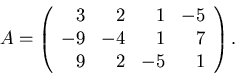
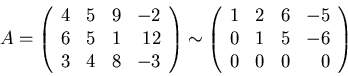
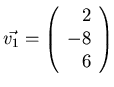 ,
,
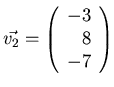 ,
,
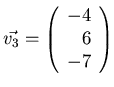 ,
,
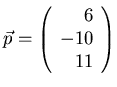 ,
and
,
and