Questions to contemplate for test #2
(first draft)
Chapter 16
- 7.
- How can you use Riemann sums to get a numerical approximation
of the integral of a function of two variables?
(You should be able to do this using either a table of values
or a graph of level curves.)
- 8.
- Interpret the meaning of the integral of a function
of two variables in terms of the (3-D) graph of z=f(x,y) and a region R in the x-y plane.
- 9.
- How are ``slices'' (i.e., cross-sections corresponding
to x=constant or y=constant) related to
iterated integrals?
- 10.
- In evaluating an iterated integral, which integration is
performed first?
- 11.
- For an iterated double integral, which limit(s) can be
functions of which variable(s)? What about for an iterated
triple integral?
- 12.
- If you are integrating a function f(x,y) over a region R in
the x-y plane, how do you determine the limits of integration?
How do you do this in reverse
(given the limits, determine the region)?
- 13.
- Consider the previous question, but now with polar coordinates.
- 14.
- Given an iterated integral in terms of x and y, how can
you rewrite it as an iterated integral in polar coordinates?
(Be sure to consider the region R,
the infinitesimal area element dA,
and the function f.)
- 15.
- Given an iterated integral polar coordinates,
how can you rewrite it as an iterated integral in
rectangular coordinates (x and y)?
(Be sure to consider the region R,
the infinitesimal area element dA,
and the function f.)
- 16.
- What do ``slices'' look like in polar coordinates? How are
they useful in writing iterated integrals in polar coordinates?
- 17.
- Explain why integrals are useful for computing totals from
given density information.
- 18.
- How can you determine the limits of integration for a triple
integral, based on a graph of the three-dimensional
region of integration?
- 19.
- What are cylindrical coordinates? When are they useful?
Describe the graphs of surfaces corresponding to r=constant,
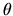 =constant, and z=constant (in cylindrical coordinates).
=constant, and z=constant (in cylindrical coordinates).
- 20.
- What are spherical coordinates? When are they useful?
Describe the graphs of surfaces corresponding to r=constant,
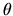 =constant, and
=constant, and 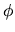 =constant (in spherical coordinates).
=constant (in spherical coordinates).
- 21.
- Given an iterated integral over a 3-D region written in
Cartesian coordinates (x and y), how do you convert it
to an integral in cylindrical coordinates?
(Be sure to consider the region of integration W,
the infinitesimal volume element dV,
and the function f.)
- 22.
- Given an iterated integral over a 3-D region written in
Carters Ian coordinates (x and y), how do you convert it
to an integral in spherical coordinates?
(Be sure to consider the region of integration W,
the infinitesimal volume element dV,
and the function f.)
++++++++ FOR TEST #3 ++++++++++++++++++++
- 6.
- What are parametric equations and how are they graphed? Can two different sets of parametric equations have the same graph?
- 5.
- How can you find the parametric equations of a circle with a given center and radius?
How can you find the parametric equations of a given line or line segment?
(How can you check that your equations are correct?)
- 4.
- If you have a set of parametric equations,
how can you find a vector which is tangent to the graph at a point?
- 3.
- What is a vector field? How is it represented graphically?
- 2.
- Given a graph of a vector field, what can you say about its components?
- 1.
- How can you relate the graph of a vector field to its formula?
Given a simple formula, how do you know something about the graph?
(For example, $\vec{F}(x,y,z)= x^2 \vec{\imath} + x^2 \vec{\jmath}$ or
$\vec{F}(x,y)= x \vec{\jmath}$ or $\vec{F}(x,y)= y \vec{\imath}$)
- 0.
- Are all vector fields gradient fields? Are all gradient fields vector fields?
- -1.
- If your parametric equations are written as $\vec{r}(t)=x(t) \vec{\imath} + y(t)\vec{\jmath} + z(t)\vec{k}$, what is $\vec{r}\;'(t)$? In what direction does it point?
About this document ...
Tamara R. Olson