Review
Sections 5.1-5.4 and 6.1-6.4
MA 1160/1161
- 1.
Given a graph of velocity vs. time, how can you estimate
the total distance traveled?
- 2.
Given a table of values of velocity as a function of time,
how can you estimate the total distance traveled?
- 3.
How do you use rectangles to get an overestimate
and/or underestimate of the area under a graph?
- 4.
Using rectangles of a fixed width to estimate the area under
a monotone function f(x) between a and b,
what is the formula for the
difference between the overestimate and the underestimate?
Explain your formula graphically.
(Why must the function be monotone?)
- 5.
What is the graphical interpretation of the integral
of a positive function? What if the function is
negative over some intervals?
- 6.
What is a Riemann sum? What is a ``left-hand sum''?
- 7.
Under what circumstances can you conclude that a
left-hand sum is an overestimate of the integral?
- 8.
How do you compute the ``average value'' of a function over
an interval?
- 9.
If you integrate the rate of change of f, what do you get?
- 10.
Given the rate of change of f(x), how could you
compute the total change in f between x=a and x=b?
- 11.
Given a formula for f'(x) how can you
compute the total change in f(x) between
two x values (say, x=a and x=b)?
- 12.
Given a graph of f'(x) and two x-values a and b,
how can you estimate f(b)-f(a)?
- 13.
Given a graph of f'(x), how can you sketch a possible
graph of f(x)?
(Why is there more than one possible graph?)
- 14.
What are the units of the integral,
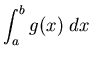 ,
in terms of the units of g and/or x?
,
in terms of the units of g and/or x?
- 15.
What is the Fundamental Theorem of Calculus?
- 16.
How can you use integrals to find the area between two curves?
- 17.
How can you tell, from a graph of y=f(x), whether
a definite integral
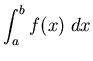 will be positive or negative?
will be positive or negative?
- 18.
What happens to the value of a definite integral
when you interchange the limits of integration?
- 19.
If two functions satisfy
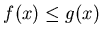 for all
x in some interval, what can you say about
their integrals? How can you explain this graphically?
for all
x in some interval, what can you say about
their integrals? How can you explain this graphically?
- 20.
Given a graph of f'(x) and a value for f(0),
how can you estimate f(2)?
- 21.
How can you ``split'' one integral into two?
- 22.
Suppose you have two different antiderivatives of f(x).
How are they related?
- 23.
If you are given f'(t) and want to know about f(t),
what does the sign (
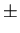 )
of f' tell you?
)
of f' tell you?
- 24.
What is ``the indefinite integral''?
How is it different from an antiderivative?
- 25.
How is an indefinite integral different from
a definite integral?
How are they related?
- 26.
For each of the differentiation formulas, what is the
corresponding integration formula?
(Exclude the product, quotient, and chain rules.)
- 27.
If you're given a differential equation, what is meant
by the ``general solution''?
Why does it involve an arbitrary constant?
- 28.
Given a differential equation and an initial condition
(or a point on the graph),
how do you find the solution? How do you check your answer?
- 29.
Given position as a function of time, how do you
find the velocity function?
- 30.
Given velocity as a function of time, how do you
find the position function?
- 31.
Suppose you know that acceleration is constant. How can
you find the velocity as a function of time?
What additional information
do you need (besides the constant rate of acceleration)?
- 32.
Suppose you know that acceleration is constant. How can
you find the position as a function of time?
What additional information
do you need (besides the constant rate of acceleration)?
- 33.
How can you define a function in terms of an integral?
What is the derivative of such a function?
- 34.
How do you find the derivative of an integral with
respect to its upper limit?
- 35.
What is the second version of the Fun. Theorem of Calculus,
and how can you use it to construct antiderivatives?
Tamara R. Olson
2002-12-12
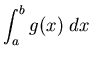 ,
in terms of the units of g and/or x?
,
in terms of the units of g and/or x? 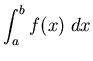 will be positive or negative?
will be positive or negative? 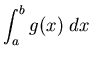 ,
in terms of the units of g and/or x?
,
in terms of the units of g and/or x? 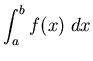 will be positive or negative?
will be positive or negative?