Things to know - Chapters 1 & 2
MA2321, Fall '03, T. Olson
Know these terms and relationships between them:
- linear equation, system of linear equations
- equivalent systems of equations
- consistent/inconsistent
- coefficient matrix, augmented matrix
- elementary row operations
- echelon form, reduced echelon form
- pivot position, pivot column
- basic variable, free variable
- vector equation
- linear combination of vectors
- span of a set of vectors
- homogeneous equation, trivial solution
- parametric vector form (of general solution)
- linear independence/dependence
- linear transformation (2 properties)
- zero matrix, identity matrix
- matrix product
- inverse matrix, invertible matrix
- column space
- null space
- basis
- partition, block
Things to think about:
- 1.
- What are the elementary row operations?
- 2.
- How do you write a system of linear equations
as a matrix equation? A vector equation?
- 3.
- What are the two ways to compute the product of
a matrix times a vector? ...a matrix times
a matrix?
- 4.
- When is matrix addition defined? ...matrix
multiplication?
- 5.
- What information can you get from the echelon form
(or reduced echelon form) of a matrix?
...of an augmented matrix?
- 6.
- How do you decide if a given vector is in the span
of another set of vectors?
- 7.
- How is the solution set of the homogeneous equation
related to the solution set of the non-homogeneous equation?
- 8.
- How do you tell if a set of vectors is linearly independent?
- 9.
- How can you find the matrix of a linear transformation?
- 10.
- Matrix algebra looks a lot like the algebra of scalar
variables. Which property(ies) do NOT hold for
matrix algebra? (e.g., distributive law, etc.)
What does this mean for solving equations?
- 11.
- How can you decide, using row reduction, if a matrix
is invertible?
- 12.
- Given an
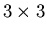 matrix A, what statements can
you write which are equivalent to saying
``The equation
matrix A, what statements can
you write which are equivalent to saying
``The equation
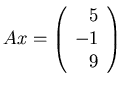 has exactly one solution''?
has exactly one solution''?
- 13.
- For a square matrix, how is invertibility
related to solving the homogeneous equation?
...non-homogeneous equations?
...the column space of the matrix?
...the null space of the matrix?
...the span of the columns?
- 14.
- How can you tell if a given vector is in the column
space of a matrix?
- 15.
- How can you tell if a given vector is in the null
space of a matrix?
- 16.
- How do you find a basis for the column space of a matrix?
- 17.
- How do you find a basis for the null space of a matrix?
- 18.
- What is meant by the questions of ``existence and uniqueness''
for solutions to
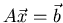 ? How are these related
to pivots in the echelon form of A?
? How are these related
to pivots in the echelon form of A?
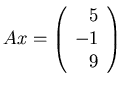 has exactly one solution''?
has exactly one solution''?
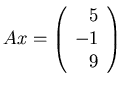 has exactly one solution''?
has exactly one solution''?