REVIEW #1 -- Multivariable Calculus
Chapters 12 and 14

The following questions are designed to get you thinking about the material. These are NOT necessarily the type of questions that you will see on the test; in fact, many probably cannot be answered adequately using only pen and paper in a one-hour test. None-the-less, these are the types of things that I'm hoping you have learned. When I grade your test, I'll be looking for evidence that you have thought about and deciphered these concepts.

1.

Besides a symbolic formula, what other ways are there to represent a function of two variables? Which representations are more useful for which purposes?

2.

Suppose you're looking at a table of values for a function of two variables (like on page 611, 612, or 630). As you read across the second row, what are you looking at? How is this related to the graph of the function?

3.

Given a set of level curves for a function, how can you tell if the function is linear?

4.

Given a table of values for a function, how can you tell if the function is linear?

5.

What is a ``cross-section'' (vertical slice)? How do you find a cross-section from a formula? What does the cross-section tell you about a graph?

6.

What is a ``level curve'' (contour)? What does the spacing of the level curves tell you about the graph?

7.

Given a table of values, how can you determine what cross-sections of the graph might look like?

8.

Given a contour plot, how can you determine what cross-sections of the graph might look like?

9.

Suppose you are looking at the graph of a function of two variables (assume it's a nice, differentiable function). What can you say about the level curves near a maximum (top of a ``hill'' on the graph)? What can you say about the cross-sections through the maximum?

10.

What equation describes the x-z plane? the x-y plane?

11.

What does the equation for a horizontal plane look like? A vertical plane?

12.

Identify at least two forms for the equation of a (non-vertical) plane. What are the meanings of all the constants in these equations?

13.

How do you find the distance from a point (x,y,z) to one of the coordinate planes? How do you find the distance to one of the coordinate axes?

14.

What is the distance equation in 3D? What is the equation for a sphere? How are these related?

15.

If you have equations for a sphere and for a plane which is parallel to some coordinate plane, how would you find the equation for their intersection (if any)? What should the intersection look like?

16.

Suppose an equation in 3D (x-y-z-space) does not involve y. What does this say about the graph? What does it say about the contour plot?

17.

Suppose you have an equation and its graph. How do you find an equation whose graph is the same, but shifted?

18.

Is it possible for level curves to cross, if they correspond to different levels?

19.

Explain why it is impossible to draw the graph of a function of three variables. If we have a function f(x,y,z) of three variables and look at contours by setting 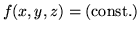$f(x,y,z)=(\mbox{const.})$, what are we drawing?

20.

What does the formula for a linear function of three variables look like? What does the formula for a linear function of two variables look like? Which of these function would have a graph which is a plane (in 3D)?

21.

Given three points on a plane (in 3D), how could you find an equation for the plane?

22.

What is a partial derivative? Given a graph of f(x,y), how can you determine where the partial derivatives are positive, negative, or zero? How are partial derivatives related to ``slices'' (cross-sections)?

23.

Given a contour plot for f(x,y), how can you estimate the partial derivative f_y at some point?

24.

Given a table of values for f(x,y), how can you estimate the partial derivative f_y at some point?

25.

Given a formula for f(x,y), how can you compute the partial derivative f_y at some point?

26.

Given a point on the graph of f(x,y), how can you find the equation for the tangent plane? How would you check your answer?

27.

How can you use partial derivatives to estimate the value of a function near a known point on its graph?

28.

Compare the following methods for estimating the value of a function f(x,y) near a known point on its graph: (1) computing the tangent plane at the known point, and then evaluating the equation for the tangent plane at the new point and (2) using the formula `` $\Delta f \approx f_x \Delta x + f_y \Delta y$.''

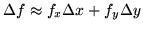29.

What is a directional derivative? How is it similar to (or different from) a partial derivative?

30.

Given a graph of f(x,y), how can you tell if a particular directional derivative is positive or negative?

31.

Given a contour plot of f(x,y), how can you tell if a particular directional derivative is positive or negative?

32.

Given a contour plot for f(x,y), how can you estimate a directional derivative at some point?

33.

Given a table of values for f(x,y), how can you estimate a directional derivative at some point?

34.

Given a formula for f(x,y), how can you compute a directional derivative at some point?

35.

What is the gradient (of a function of two variables)? In what direction does it point? What is the meaning of its magnitude (length)?

36.

Given a contour plot for f(x,y), how can you estimate the direction of the gradient at a point? How can you estimate its magnitude?

37.

Consider the graph of any equation in three variables, which gives a surface in space. Compare the two different ways of interpreting this graph ...as the graph of a function of two variables f(x,y) or as a level surface for a function of three variables, F(x,y,z).

• How are the equations for these functions related?
• How would you use each to find a vector parallel to the surface at a given point?
• How would you use each to find a vector perpendicular to the surface at a given point?
• Interpret the gradient, 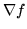$\nabla f$, graphically.
• Interpret the gradient, 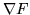$\nabla F$, graphically.

38.

For a function of three variables, F(x,y,z), how do you find the gradient symbolically? How is it related to the level surfaces of F?

39.

For a function of three variables, F(x,y,z), how can you compute a directional derivative at a point? What does it mean?

40.

Suppose you have a function of three (independent) variables, which are themselves functions of six other (independent) variables. How do you use the chain rule (which terms are added and which multiplied, and how many are there?)? What does the chain rule tell you?

41.

Consider the second-order partial derivatives 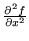$\frac{\partial^2 f}{\partial x ^2}$ and $\frac{\partial^2 f}{\partial y ^2}$.

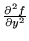(a)

How do you compute these symbolically?

(b)

How can you interpret them graphically (i.e., what do they say about the 3-D graph z=f(x,y)?)?

(c)

How would you estimate their sign (positive, negative, or zero) based on the level curves of f?

(d)

What are the units associated with them?

42.

Consider the second-order partial derivatives 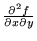$\frac{\partial^2 f}{\partial x \partial y}$ and $\frac{\partial^2 f}{\partial y \partial x}$.

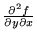(a)

How do you compute these symbolically?

(b)

How can you interpret them graphically (i.e., what do they say about the 3-D graph z=f(x,y)?)?

(c)

How would you estimate their sign (positive, negative, or zero) based on the level curves of f?

(d)

What are the units associated with them?

(e)

How are they related (assuming they are continuous)?