-
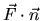 is constant?
is constant?
-
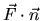 is not constant, but S is
parallel to one of the coordinate planes?
is not constant, but S is
parallel to one of the coordinate planes?
- S is a piece of a sphere?
- S is a piece of a vertical cylinder?
- S is the graph of a function z=f(x,y)?
Questions up to the plus signs ("++++++++") will be covered on our
Test #3.