REVIEW #3 --
18.1-18.4, 19.1, 20.1-20.4
T. Olson
Questions past the plus signs ("++++++++") will be covered on our Test #3.
- 1.
- What are parametric equations and how are they graphed?
Can two different sets of parametric equations have
the same graph?
- 2.
- How can you find the parametric equations of a circle with
a given center and radius?
How can you find the parametric equations of
a given line or line segment?
(How can you check that your equations are correct?)
- 3.
- If you have a set of parametric equations, how can you find
a vector which is tangent to the graph at a point?
- 4.
- What is a vector field? How is it represented graphically?
- 5.
- Given a graph of a vector field, what can you say about
its components?
- 6.
- How can you relate the graph of a vector field to its formula?
Given a simple formula, how do you know something about the graph?
(For example,
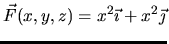 or
or
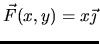 or
or
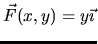 )
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
)
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
- 7.
- If your parametric equations are written as
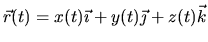 ,
what is
,
what is
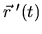 ? In what direction does it point?
? In what direction does it point?
- 8.
- What does a line integral measure? How would you estimate
the sign (positive, negative, zero) based on a graph?
- 9.
- How do you compute the line integral of a vector field along
a given curve?
- 10.
- Is every gradient field a vector field?
Is every vector field a gradient field?
- 11.
- If you're given a formula for a vector field, how can
you decide if
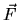 it is a gradient field? (There are
at least 2 ways).
it is a gradient field? (There are
at least 2 ways).
- 12.
- How is a gradient field related to level curves? How can you
use this to graphically check whether a given vector
field is a gradient field?
- 13.
- What does it mean for a vector field to be ``path independent''?
What does this mean in terms of circulation?
How is this related to gradient fields?
- 14.
- What is a potential function? Which vector fields have one?
- 15.
- What is Green's theorem? How do you use it?
When does it NOT hold?
- 16.
- What does a flux integral measure? How can you estimate the
sign of one (positive, negative, or zero), given the graph
of a vector field and an oriented surface?
- 17.
- How do you compute the flux of a given vector field
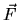 through a given surface S, when
through a given surface S, when
-
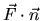 is constant?
is constant?
-
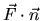 is not constant, but S is
parallel to one of the coordinate planes?
is not constant, but S is
parallel to one of the coordinate planes?
- 18.
- What is the divergence of a vector field? Is it a scalar or vector?
What is the formula for it? What does it mean in terms of ``flows''?
- 19.
- What is the curl of a vector field? Is it a scalar or vector?
What is the formula for it? What does it mean in terms of ``flows''?
- 21.
- What is the ``circulation density of
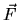 about
about 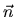 ''?
How is it related to the curl?
''?
How is it related to the curl?
- 17.
- How do you compute the flux of a given vector field
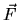 through a given surface S, when
through a given surface S, when
- S is a piece of a sphere?
- S is a piece of a vertical cylinder?
- S is the graph of a function z=f(x,y)?
- 20.
- What is the divergence theorem? When is it NOT valid?
State in words what the divergence theorem says.
- 22.
- What is Stokes' theorem? When is it NOT valid?
State in words what Stokes' theorem says.
About this document ...
Tamara R. Olson
trolson at mtu.edu
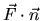 is constant?
is constant?
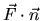 is not constant, but S is
parallel to one of the coordinate planes?
is not constant, but S is
parallel to one of the coordinate planes?