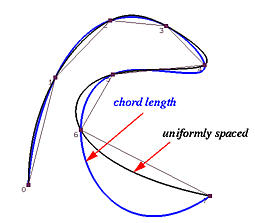
The Chord Length Method

If an interpolating curve follows very closely to the data polygon, the length of the curve segment between two adjacent data points would be very close to the length of the chord of these two data points, and the the length of the interpolating curve would also be very close to the total length of the data polygon. In the figure below, each curve segment of an interpolating polynomial is very close to the length of its supporting chord, and the length of the curve is close to the length of the data polygon. Therefore, if the domain is subdivided according to the distribution of the chord lengths, the parameters will be an approximation of the arc-length parameterization. This is the merit of the chord length or chordal method.

Suppose the data points are D₀, D₁, ..., D_n. The length between D_i-1 and D_i is |D_i-D_i-1|, and the length of the data polygon is the sum of the lengths of these chords:

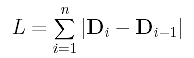
Therefore, the ratio of the chord length from data point D₀ to data point D_k, denoted as L_k, over the length of the data polygon is

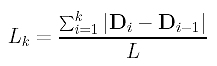
If we prefer to have an arc-length parameterization of the interpolating curve, the domain has to be divided according to the ratio L_k. More precisely, if the domain is [0,1], then parameter t_k should be located at the value of L_k:

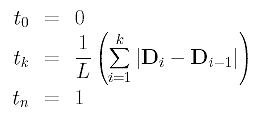
where L is the length of the data polygon. In this way, the parameters divide the domain into the ratio of the chord lengths.

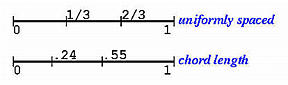
Let us look at an example. Suppose we have four data points (n = 3): D₀ = < 0,0 >, D₁ = < 1,2 >, D₂ = < 3,4 > and D₃ = < 4,0 >. The length of each chord is

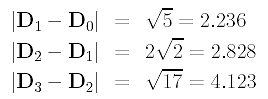
and the total length is

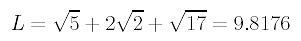
Finally, we have the corresponding parameters:

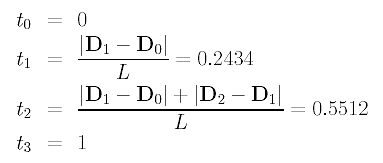
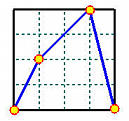
The following figures show the data points and the parameter distributions of the uniformly spaced method and the chord length method.

What if the domain is [a,b] rather than [0,1]? Note that L_k is a ratio between 0 and 1. Since the length of [a, b] is b-a, L_k(b-a), 0 <= k <= n, divide [0,b-a] into the same ratio as we did for [0,1]. Therefore, the following parameters divide [a,b] according to the chord lengths:

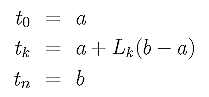
The chord length method is widely used and usually performs well. Since it is known (proved by R. Farouki and also well-known in geometry) that polynomial curves cannot be parameterized to have unit speed (i.e., arc-length parameterization), the chord length can only be an approximation. Sometimes, a longer chord may cause its curve segment to have a bulge bigger than necessary. In the figure below, the black and blue curves both interpolate 7 data points. As you can see, both curves have very similar shape, except for the last segment, and the one computed with chord length method wiggling a little. The last curve segments are very different and the curve using the chord length method has a large bulge and twists away from the red curve produced by the uniformly spaced method. This is a commonly seen problem with the chord length method.