The Vigenère Cipher: User Guide


| Since the software is being updated frequently, the images on this guide page may not be up-to-date. However, most changes and differences will be minor. |
This program, VIGvisual, is designed to support the activities discussed on previous pages. It has three tabs: Demo, Practice and Attack. The Demo tab provides an animated demonstration of the Vigenère cipher. The Practice tab offers a chance for the user to practice encryption and decryption operations. The Attack tab has Kasiski's method and the Index of Coincidence (IOC) method for estimating a possible length of the unknown keyword, and the χ2 method to recover the keyword given the length estimation. To break the Vigenère cipher completely, a number of iterations and other skills would be needed.


In an encryption session with user input, the user enters the plaintext and keyword and the system fills in the ciphertext when clicking Encrypt. In a decryption session with user input, the user enters the ciphertext and keyword and the system fills in the plaintext when clicking Decrypt.
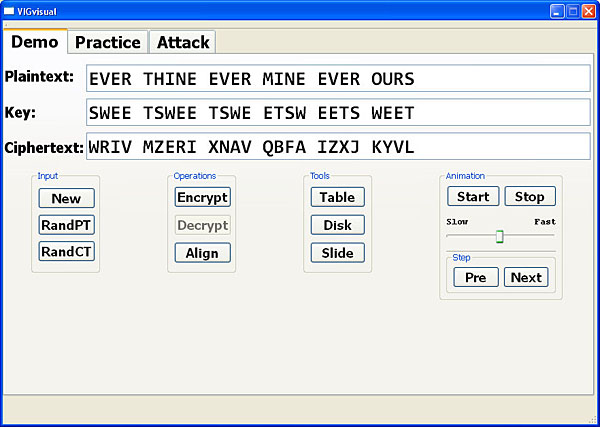
By default, the keyword is repeated and aligned with the original word structure as shown above. Clicking Align switches to the view of breaking the plaintext/ciphertext to align with the keyword as shown below.
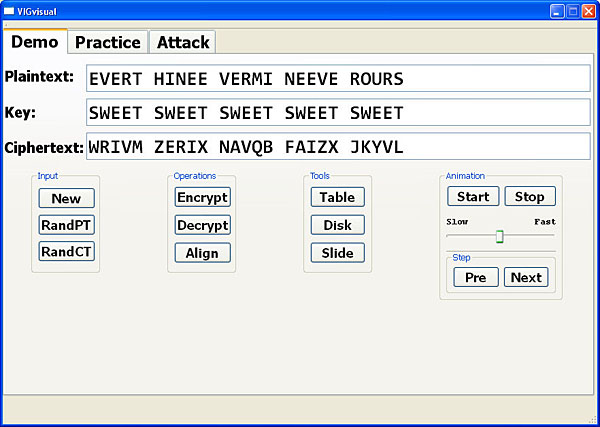
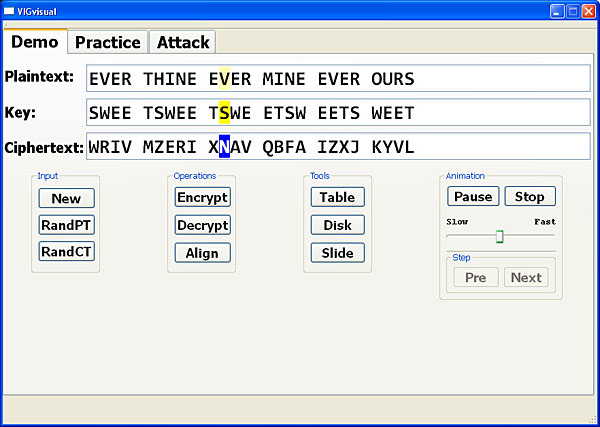
During an animation, the user may place the cursor between any two letters in the plaintext, keyword or ciphertext, and the animation will continues with the next letter. Moreover, the user may click Pause to suspend the animation and the Pre and Next buttons become available. The user may click between two letters in the plaintext, keyword or ciphertext, followed by Pre (resp., Next) to move to the previous (resp., next) position. In this way, the user is able to move to anywhere in the text and step through the encryption or decryption process. Click Resume to resume the animation and Stop to end it.
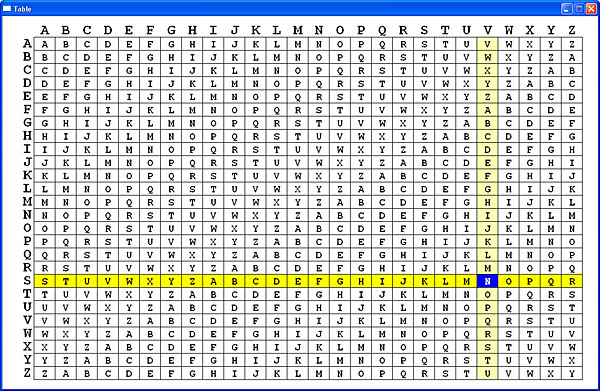
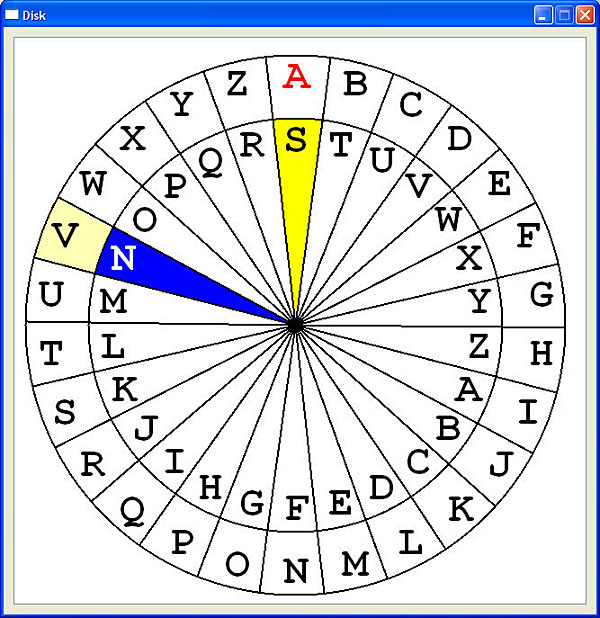

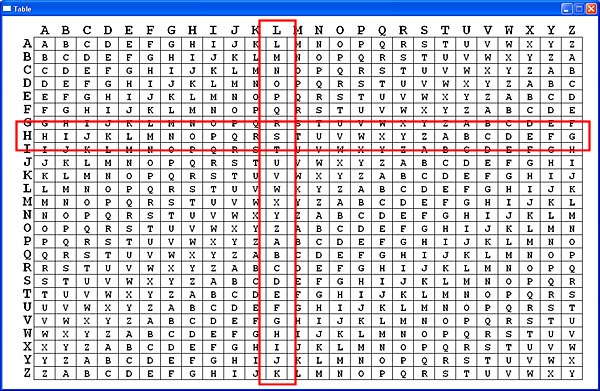
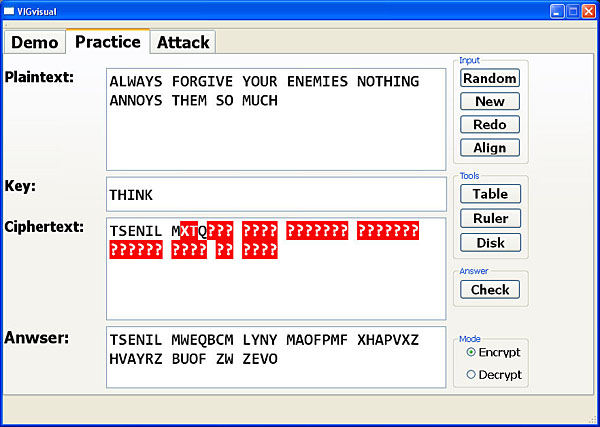
To perform a practice, the user may bring up the Vigenère table, disk or slide. For example, consider the second letter L in the plaintext ALWAYS.... It is encrypted by the second letter H. The corresponding letter in the ciphertext is found at the intersection of row H (keyword letter) and column L (plaintext letter). The result is S.
To use the cipher disk, rotate the top disk by dragging until the keyword letter H aligns with the letter A of the bottom disk. Then, the corresponding plaintext and ciphertext letters are on the bottom and top disks, respectively. Hence, the plaintext letter L is encrypted to the ciphertext letter S. Conversely, the ciphertext letter S is decrypted by the keyword letter H to the plaintext letter L.

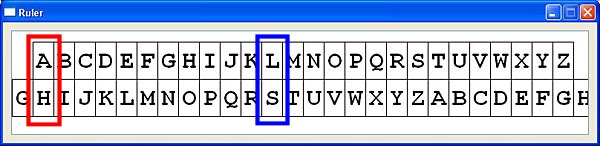
To use the slide, slide the lower part left and right by dragging until the keyword letter H aligns with the letter A of the top fixed part. Then, the corresponding plaintext and ciphertext letters are on the top and bottom part, respectively. Hence, the plaintext letter L is encrypted to the ciphertext letter S. Conversely, the ciphertext letter S is decrypted by the keyword letter H to the plaintext letter L.
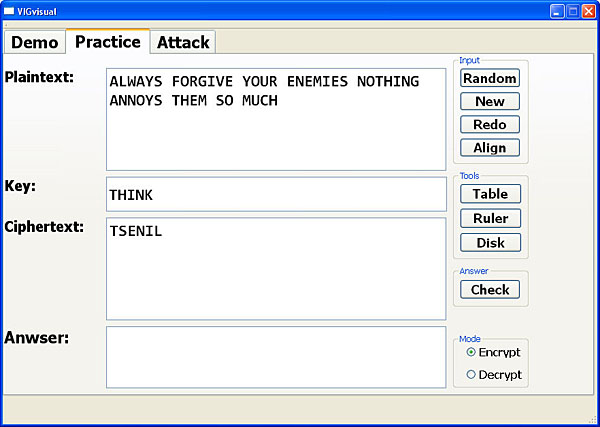
You may stop the encryption/decryption process at any time and click the Check button. Then, the correct answer is shown in the Answer area, and each incorrect letter in the plaintext or ciphertext area is shown in red or a question mark if there is no input for that letter. Note that once clicking Check you are not able to make changes to the keyword and plaintext/ciphertext. Click Redo to modify the keyword or plaintext/ciphertext, or click Random or New to start a new session.
Use the New button to clear the ciphertext area and enter your ciphertext. Or, use the Random button to generate a randomly selected ciphertext:
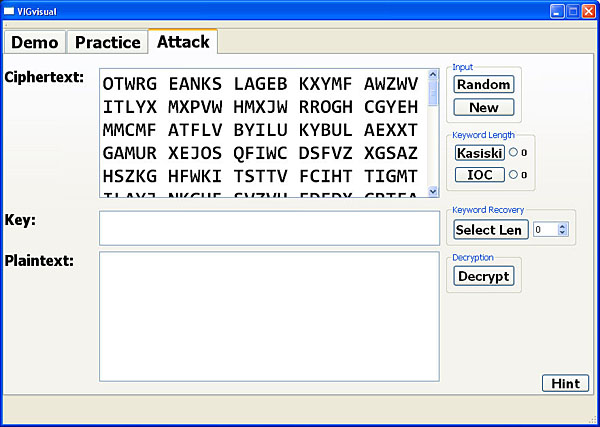
This tab has Kasiski's Method and the Index of Coincidence method for estimating the length of the unknown keyword. Use the Kasiski (resp., IOC) button to bring up the Kasiski's method (resp., Index of Coincidence) window. The estimated keyword length is shown next to that method's button.
The Algorithm button brings up a window showing the procedure for breaking the Vigenère cipher.

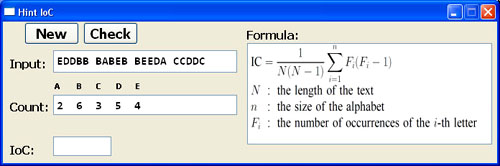
The IOC button brings up the IOC hint window as shown in the first image below. Click the New button to generate an input on a 5-letter alphabet (i.e., A, B, C, D and E) and the count of each letter. The system expects the user to fill in the Index of Coincidence of this string in the IoC field. The user may click the Check button to the answer next to the input field.


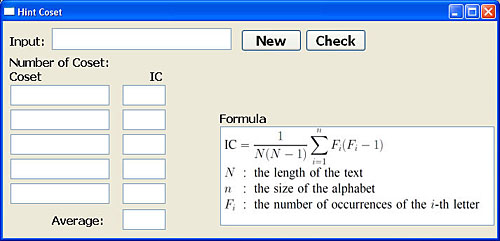
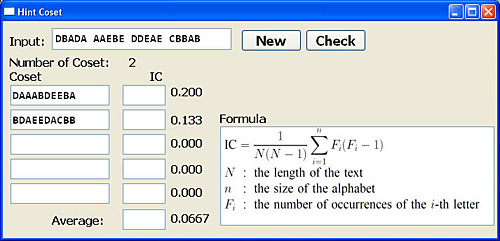
The Coset button brings up the coset hint window as shown below. Click the New to generate a short string and the number of cosets. The system expects the user to enter the coset and the index of coincidence of that coset in the Coset and IC fields, and the average of all index of coincidence values in the Average field. The user may click the Check button to see the answer of each field.
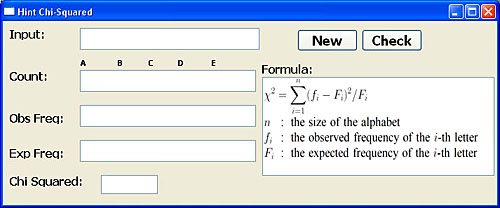
The Chi-Squared button brings up the χ2 hint window. Click the New button to generate a short string and the letter counts, observed (Obs) frequencies and expected frequencies (Exp). The system expects the use to compute and enter the χ2 in the Chi Squared field. The user may click Check to see the answer,


The following is the Kasiski window:
The lower right corner has a Hint button. Clicking it brings up the procedure of Kasiski's method as shown below.

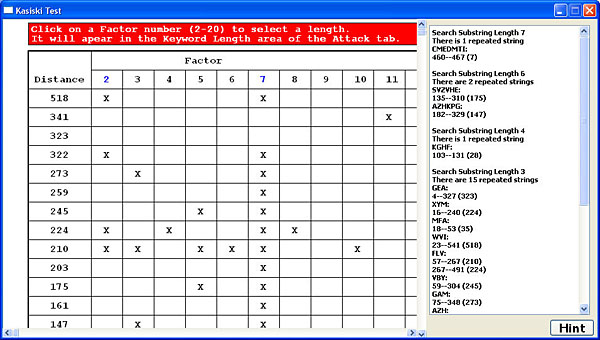
The right panel of this window shows all repeated strings found in the ciphertext and the left panel shows the distances and their factors, and the count of each factor (See the Kasiski's Method page).
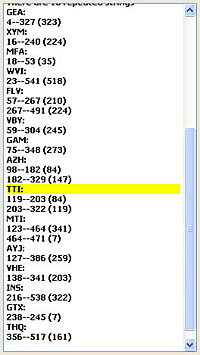
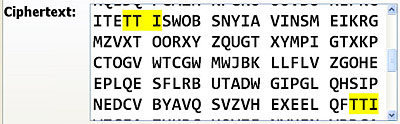
Clicking a repeated string highlights it in the ciphertext area of the Attack tab. The right figure below shows the repeated string TTI is selected and the left figure shows the highlighted ciphertext. Since this string appears in three places (i.e., positions 119, 203 and 322), you may have to scroll up and down to see the result. If you click the positions (e.g., 119-203(84)), only the repeated string in positions 119 and 203 are shown.
 |
 |
 |
Scroll up and down (and left and right) of the left panel and find the factor corresponding to the largest count (i.e., the most common one). This factor is usually a good estimate of the length of the unknown keyword. The following figure shows that the largest count is 16 which corresponds to the factor 7. Click on the factor to export it to the Attack tab. This means you have found a possible length. If you wish to use a different keyword length, clicking on the Kasiski button will bring you back to this table for you to select a different length.
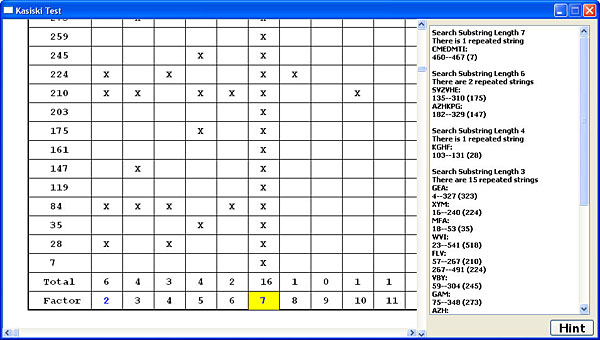
Once a length is selected, its value appears next to the Kasiski button of the Attack tab:

Two Important Notes
|

The lower right corner has a Hint button. Clicking it brings up the procedure of applying index of coincidence to each coset to find a possible keyword length.

The second column of this table only shows a portion of each coset. Clicking on a coset will show the complete coset in the bottom area.

This system shows the largest three index of coincidence values in blue on the fourth column. In general, the length corresponding to the largest average value works fine. Scroll this table to the bottom to find the largest average index of coincidence, and click the length value to select and export it. The following figure shows that the length of 7 is selected.
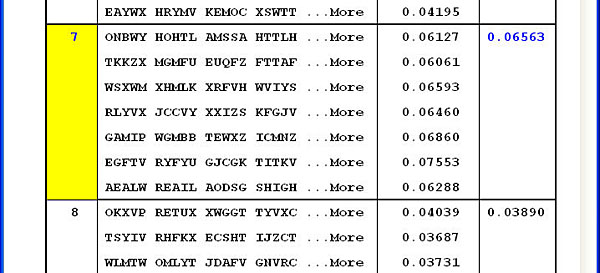
Once a length is selected, its value appears next to the IOC button of the Attack tab:


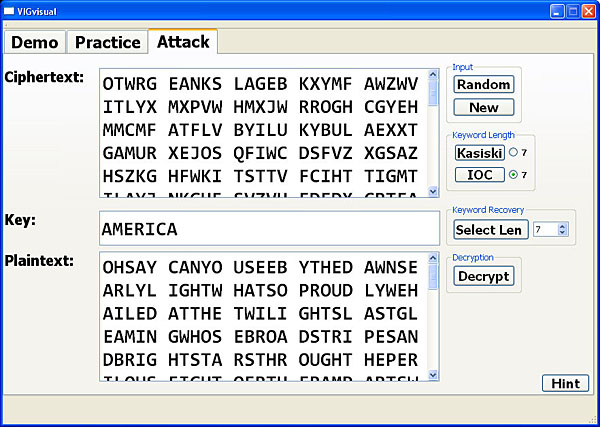
After an estimation is chosen, clicking the Select Len button brings up the Keyword Recovery window as shown below. This window has two portions. Each column of the top portion has the χ2 values of each coset, and each row corresponds to the shift of a letter. For example, the χ2 value of shifting the first coset to G is 5.11, the χ2 value of shifting the second coset to G is 20.8, etc. The smallest χ2 of each coset (i.e., column) is shown in blue, and the letter corresponding to the smallest χ2 of each coset is shown in the Key row. The following table shows the possible keyword being AMERICA
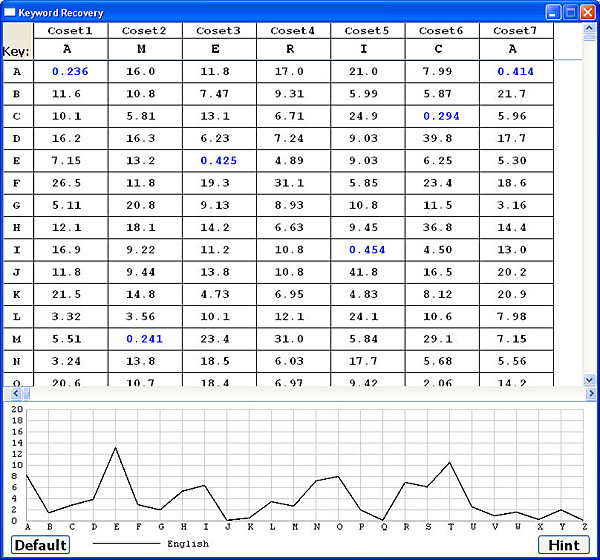
Scrolling the top portion to the bottom, you will see the current keyword and a portion of the decrypted text:

The recovered keyword also appears in the Key field of the Attack tab as shown below.

The lower right corner of the Keyword Recovery window has a Hint button. Clicking it brings up the procedure of applying the χ2 method to recover the unknown keyword.

The recovered keyword may not be correct, and, in this case, you have to modify it in order to correctly decrypt the ciphertext. VIGvisual shows at most three frequency graphs at any time for this purpose. Initially, the bottom part of the Keyword Recovery window shows the English frequency graph:
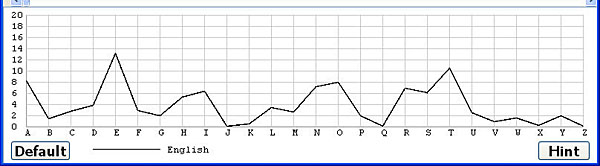
The horizontal axis of this graph has the 26 letters and the vertical axis shows the percentage values from 0% to 20%. Since each letter in the recovered keyword corresponds to a coset, click the coset number to select that coset to modify. For example, coset 4, which corresponds to R, is selected and is highlighted as shown below. At the same time, the frequency graph of the R shift is shown. Note that the frequency graph of the R shift matches the trend of the English frequency very well.

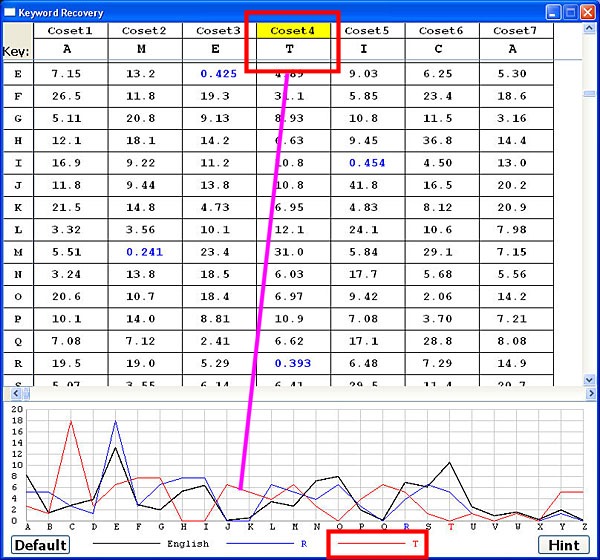
Suppose that you do not think the R shift is the right choice. Click the letter below the horizontal axis you wish to use and the frequency graph of that letter appears. Moreover, the corresponding letters in the keyword in this window and the keyword in the Attack tab also change. In the following image, the letter T is selected. It appears in the Key field and the frequency graph of the T shift is shown. This T shift frequency graph does not match the English frequency very well. As a result, the T shift is unlikely to be a correct choice. In general, if the frequency graph of a shift matches the English frequency well, the corresponding χ2 is small. Of course, the frequency graph that can generate the smallest χ2 matches the English frequency better than other shifts. However, in many cases the shift that corresponds to the smallest χ2 is not the best choice, and you have to edit the recovered keyword to find another letter. Usually, trying a few of the smallest χ2 values and checking their frequency graphs can provide additional information for selecting a correct keyword.
The frequency graph of English and the frequency graph of the smallest χ2 are always shown. Clicking any letter causes a new (i.e., the third) graph to appear and this graph will be replaced by future graphs.
Except for the English frequency graph the computed frequency graph of a coset shifts to the left or right as you click on letters. For example, the following shows the frequency graphs of U, V, W, X and Y. The peak at letter E of the correct shift R shifts to the position of C (i.e., two positions to the left of E) when the letter T (i.e., two positions to the right of R) is selected. As we move to the right from U to Y, the peak moves to the left from B to X in a cyclic way.


The Default button restores the keyword back to the one corresponding to the smallest χ2 values.
Example 1
Let us take a look at an example to illustrate the editing using frequency graphs.
Example 3 on the
Complete Examples page has the following ciphertext:
LPROZ OOGRJ ZGFLV TUKMC WFDQM PZXIJ LVRWQ XEOSZ ZHTEK UYSCR
PTFCZ UHXIJ LPPTD CPRBY OSMGY TLEVD UAQMF IFMZV LVYTO QDLHX
LBPLL KYCQY ODRKS ACTEU XZEVO UAQMF OSDSU BKMBJ QEORF WFQCK
HKSOD INGJZ SHGVV LMSZD WWHFJ AVQGF NUWMW AOIXT CSRYC YPPTP
LFUCR AVQHR RVRES QCKHM LGARF YHXZP CSNWS NCRQV GHRLR ZEDHF
JVUPC XZJQC ATISQ SCGXN BALWY MAQCY OSD
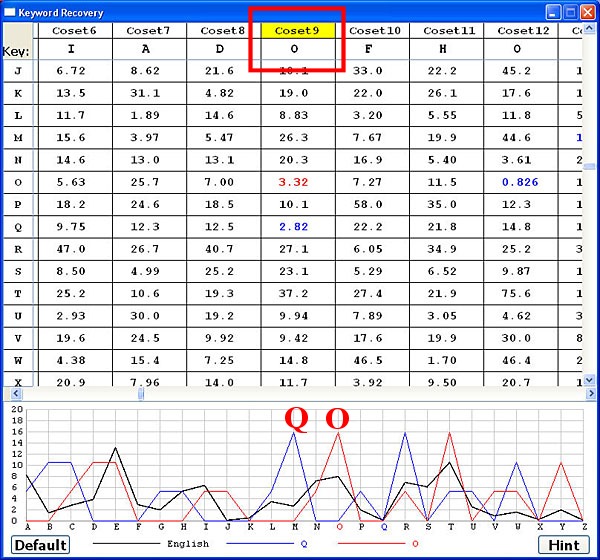
The recovered keyword with the χ2 method is THEILIADQFHOMER, which looks like "THE ILIAD QF HOMER"" and the letter Q is not right. The following image shows the frequency graph of the Q shift.
If you look at the χ2 values, you should see that the shift of Q has the smallest χ2 of coset 9 (2.82) and the next smallest χ2 value is the O shift (3.32). Click O in the frequency graph and its frequency graph appears. Now, it is clear that the frequency graph of O matches the trend of the English frequency better than the shift of Q does. As a result, the keyword should be "THE ILIAD OF HOMER". ♦
The following is the actual plaintext with spaces and punctuation added:
O say can you see by the dawn's early light,
What so proudly we hailed at the twilight's last gleaming,
Whose broad stripes and bright stars through the perilous fight,
O'er the ramparts we watched, were so gallantly streaming?
And the rockets' red glare, the bombs bursting in air,
Gave proof through the night that our flag was still there;
O say does that star-spangled banner yet wave,
O'er the land of the free and the home of the brave?


|

|

|