Heron's Formula for Computing Triangle Area Using External Functions

Problem Statement

We have seen Heron's formula for computing triangle area using internal functions. This problem uses the same idea; but the program should use external functions.

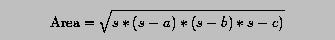
Given a triangle with side lengths a, b and c, its area can be computed using the Heron's formula:

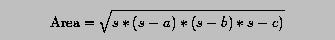
where s is the half of the perimeter length:

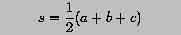
In order for a, b and c to form a triangle, two conditions must be satisfied. First, all side lengths must be positive:

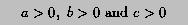
Second, the sum of any two side lengths must be greater than the third side length:

Write a program to read in three real values and use a function for testing the conditions and another function for computing the area. Should the conditions fail, your program must keep asking the user to re-enter the input until the input form a triangle. Then, the other function is used to compute the area.

Solution

! --------------------------------------------------------------------
!    This program uses Heron's formula to compute the area of a
! triangle.  It "contains" the following functions;
!    (1)  LOGICAL function TriangleTest() -
!         this function has three real formal arguments and tests
!         to see if they can form a triangle.  If they do form a
!         triangle, this function returns .TRUE.; otherwise, it
!         returns .FALSE.
!    (2)  REAL function TriangleArea() -
!         this functions has three real formal arguments considered
!         as three sides of a triangle and returns the area of this
!         triangle.
! --------------------------------------------------------------------

PROGRAM  HeronFormula
   IMPLICIT  NONE

   INTERFACE
      LOGICAL FUNCTION  TriangleTest(a, b, c)
         REAL, INTENT(IN) :: a, b, c
      END FUNCTION  TriangleTest

      REAL FUNCTION  Area(a, b, c)
         REAL, INTENT(IN) :: a, b, c
      END FUNCTION  Area
   END INTERFACE

   REAL :: a, b, c, TriangleArea

   DO
      WRITE(*,*)  'Three sides of a triangle please --> '
      READ(*,*)   a, b, c
      WRITE(*,*)  'Input sides are ', a, b, c
      IF (TriangleTest(a, b, c))  EXIT  ! exit if not a triangle
      WRITE(*,*)  'Your input CANNOT form a triangle.  Try again'
   END DO

   TriangleArea = Area(a, b, c)
   WRITE(*,*)  'Triangle area is ', TriangleArea

END PROGRAM  HeronFormula

! --------------------------------------------------------------------
! LOGICAL FUNCTION  TriangleTest() :
!    This function receives three REAL numbers and tests if they form
! a triangle by testing:
!    (1)  all arguments must be positive, and
!    (2)  the sum of any two is greater than the third
! If the arguments form a triangle, this function returns .TRUE.;
! otherwise, it returns .FALSE.
! --------------------------------------------------------------------

LOGICAL FUNCTION  TriangleTest(a, b, c)
   IMPLICIT  NONE

   REAL, INTENT(IN) :: a, b, c
   LOGICAL          :: test1, test2

   test1 = (a > 0.0) .AND. (b > 0.0) .AND. (c > 0.0)
   test2 = (a + b > c) .AND. (a + c > b) .AND. (b + c > a)
   TriangleTest = test1 .AND. test2  ! both must be .TRUE.
END FUNCTION  TriangleTest

! --------------------------------------------------------------------
! REAL FUNCTION  Area() :
!    This function takes three real number that form a triangle, and
! computes and returns the area of this triangle using Heron's formula.
! --------------------------------------------------------------------

REAL FUNCTION  Area(a, b, c)
   IMPLICIT  NONE

   REAL, INTENT(IN) :: a, b, c
   REAL             :: s

   s    = (a + b + c) / 2.0
   Area = SQRT(s*(s-a)*(s-b)*(s-c))
END FUNCTION  Area

Click here to download this program.

Program Input and Output

The following is the output from the above program.

Three sides of a triangle please --> 
-3.0  4.0  5.0
Input sides are -3.,  4.,  5.
Your input CANNOT form a triangle.  Try again
Three sides of a triangle please --> 
1.0  3.0  4.0
Input sides are 1.,  3.,  4.
Your input CANNOT form a triangle.  Try again
Three sides of a triangle please --> 
6.0  8.0  10.0
Input sides are 6.,  8.,  10.
Triangle area is 24.

Discussion

External LOGICAL function TriangleTest() receives three REAL values. The result of the first test condition is saved to a local LOGICAL variable test1, while the result of the second condition is saved to another LOGICAL variable test2. Since both conditions must be true to have a triangle, test1 and test2 are .AND.ed and the result goes into the function name so that it could be returned.
External REAL function Area is simple and does not require further discussion.
The main program has a DO-EXIT-END DO loop. In each iteration, it asks for three real values. These values are sent to LOGICAL function TriangleTest() for testing. If the returned value is .TRUE., the input form a triangle and the control of execution exits. Then, the area is computed with REAL function Area(). If the returned value is .FALSE., a message is displayed and loops back asking for a new set of values.

To provide the main program with all information for using the two external functions, an interface block is inserted in the beginning:

INTERFACE
   LOGICAL FUNCTION  TriangleTest(a, b, c)
      REAL, INTENT(IN) :: a, b, c
   END FUNCTION  TriangleTest

   REAL FUNCTION  Area(a, b, c)
      REAL, INTENT(IN) :: a, b, c
   END FUNCTION  Area
END INTERFACE