Factorial and Combinatorial Coefficient

Problem Statement

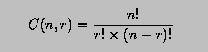
The combinatorial coefficient C(n,r) is defined as follows:

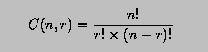
where 0 <= r <= n must hold. Write a module that contains two functions: (1) Factorial() and (2) Combinatorial(). The former computes the factorial of its argument, while the latter uses the former to compute the combinatorial coefficient. Then, write a main program that uses this module.

Solution

! --------------------------------------------------------------------
! MODULE  FactorialModule
!    This module contains two procedures: Factorial(n) and
! Combinatorial(n,r).  The first computes the factorial of an integer
! n and the second computes the combinatorial coefficient of two
! integers n and r.
! --------------------------------------------------------------------

MODULE  FactorialModule
   IMPLICIT  NONE

CONTAINS

! --------------------------------------------------------------------
! FUNCTION  Factorial() :
!    This function accepts a non-negative integers and returns its
! Factorial.
! --------------------------------------------------------------------

   INTEGER FUNCTION  Factorial(n)
      IMPLICIT  NONE

      INTEGER, INTENT(IN) :: n          ! the argument
      INTEGER             :: Fact, i    ! result

      Fact = 1                          ! initially, n!=1
      DO i = 1, n                       ! this loop multiplies
         Fact = Fact * i                ! i to n!
      END DO
      Factorial = Fact

   END FUNCTION  Factorial

! --------------------------------------------------------------------
! FUNCTION  Combinarotial():
!    This function computes the combinatorial coefficient C(n,r).
! If 0 <= r <= n, this function returns C(n,r), which is computed as
! C(n,r) = n!/(r!*(n-r)!).  Otherwise, it returns 0, indicating an
! error has occurred.
! --------------------------------------------------------------------

   INTEGER FUNCTION  Combinatorial(n, r)
      IMPLICIT  NONE

      INTEGER, INTENT(IN) :: n, r
      INTEGER             :: Cnr

      IF (0 <= r .AND. r <= n) THEN     ! valid arguments ?
         Cnr = Factorial(n) / (Factorial(r)*Factorial(n-r))
      ELSE                              ! no,
         Cnr = 0                        ! zero is returned
      END IF
      Combinatorial = Cnr

   END FUNCTION  Combinatorial

END MODULE  FactorialModule

Here is the main program:

! --------------------------------------------------------------------
! PROGRAM  ComputeFactorial:
!    This program uses MODULE FactorialModule for computing factorial
! and combinatorial coefficients.
! --------------------------------------------------------------------

PROGRAM  ComputeFactorial
   USE       FactorialModule            ! use a module

   IMPLICIT  NONE

   INTEGER :: N, R

   WRITE(*,*)  'Two non-negative integers --> '
   READ(*,*)   N, R

   WRITE(*,*)  N,   '! = ', Factorial(N)
   WRITE(*,*)  R,   '! = ', Factorial(R)

   IF (R <= N) THEN                     ! if r <= n, do C(n,r)
      WRITE(*,*)  'C(', N, ',', R, ') = ', Combinatorial(N, R)
   ELSE                                 ! otherwise, do C(r,n)
      WRITE(*,*)  'C(', R, ',', N, ') = ', Combinatorial(R, N)
   END IF

END PROGRAM  ComputeFactorial

Program Input and Output

Two non-negative integers -->
13  4
13! = 1932053504
4! = 24
C(13,4) = 221

Discussion

• The computation of combinatorial coefficients has been discussed in an programming example, where functions Cnr(n,r) and Factorial(k) are internal functions of the main program.
• In this version, functions Factorial(n) and Combinatorial(n,r) are moved to a module called FactorialModule as internal functions of that module.
• Factorial(n) takes a non-negative integer and returns its factorial.
• Combinatorial(n,r) takes two non-negative integers n and r. If 0 <= r <= n, the combinatorial coefficient C(n,r) is returned; otherwise, 0 is returned.
• Note that in module FactorialModule, there is no variables global to its internal functions. All internal functions use their own internal (or local) variables.
• This module does not perform many checks as in a previous programming example. But, it is not difficult to add these tests.
• After moving the computation functions to a module, the main program becomes simpler. In the beginning, the main program must USES FactorialModule so that functions Factorial() and Combinatorial() can be accessed from within the main program.
• The main program reads in values for n and r. If r <= n, the combinatorial coefficient C(n,r) is computed by calling Combinatorial(n,r); otherwise, the main program computes Combinatorial(r,n).
• If the main program and module FactorialModule are stored in files fact-1p.f90 and fact-m.f90, respectively, then you can compile them together with the following command:

  f90 fact-m.f90 fact-1p.90
  

  or with the following that generates an executable called fact1p:

  f90 fact-m.f90 fact-1p.90 -o fact-1p