


Next: The geometry
Up: Class room note: Drawing
Previous: History and motivation
The algebra
Consider five equally spaced line segments meeting at a point B.
The angels formed will be
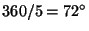 angles. Thus
we will need to construct
angles. Thus
we will need to construct
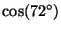 using our straight-edge,
sring and chalk.
Recall that in radians
using our straight-edge,
sring and chalk.
Recall that in radians
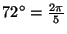 .
Let
.
Let
then
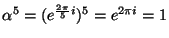 .
Hence
.
Hence 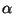 is a root of the polynomial
X5-1 = (X-1)(1+X+X2+X3+X4).
Thus, because
is a root of the polynomial
X5-1 = (X-1)(1+X+X2+X3+X4).
Thus, because
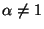 ,
we have
,
we have
Also
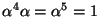 ,
So
,
So
because
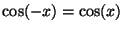 and
and
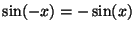 .
Let
.
Let
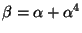 .
Then
.
Then
We need to construct 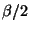 .
Now
.
Now
Therefor 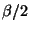 and hence
and hence
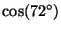 is a root of
is a root of
4X2+2X-1
a quadratic. Thus
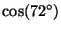 can be drawn bye inscribing
straight lines and circles. Note in particular applying
the quadratic formula we have
can be drawn bye inscribing
straight lines and circles. Note in particular applying
the quadratic formula we have
Thus we need to construct this length.
Donald L. Kreher
2002-10-01