Next: Acknowledgements
Up: Class room note: Drawing
Previous: The algebra
In Section 2 we showed that we need to construct
The only tools we have available are a straight edge with no marks
some string and a piece of chalk. Thus given two points
we can draw a straight line through them and we can draw a circle
centered at one of the points that passes through the other.
Furthermore using the compass (string and chalk) we can
- i
- erect a perpendicular to line at a point on the line;
- ii
- bisect a line segment; and
- iii
- copy the distance between two marked points on one line
to another line.
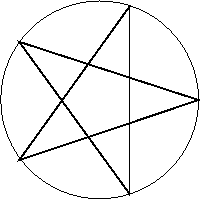
The 7 steps to construct the pentagram are:
- 1.
- Mark any two points A and B and draw a line
 through them.
Draw a circle of radius |AB| centered at B.
Let C be the the point other than A where the circle intersects
through them.
Draw a circle of radius |AB| centered at B.
Let C be the the point other than A where the circle intersects  .
Take AB to be our unit length, i.e. the length |AB|=1.
.
Take AB to be our unit length, i.e. the length |AB|=1.
- 2.
- Bisect AB at D and DB at E.
- 3.
- Erect a line perpendicular to
 at E and mark off
F on it such that
|EF| = |AD|. Note that
the Pythagorian formula shows that
at E and mark off
F on it such that
|EF| = |AD|. Note that
the Pythagorian formula shows that
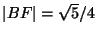 .
.
- 4.
- Mark G on
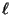 such that
|EG|= |BF|
such that
|EG|= |BF|
- 5.
- Erect a line perpendicular to
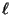 at G and Let Hbe the point where it intersects the circle.
The angle
at G and Let Hbe the point where it intersects the circle.
The angle
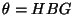 is
is 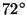 s. To see this observe
that
s. To see this observe
that
- 6.
- Using arc CH mark off the vertices of
the pentagram.
- 7.
- Draw the pentagram.



Next: Acknowledgements
Up: Class room note: Drawing
Previous: The algebra
Donald L. Kreher
2002-10-01
![\begin{picture}(3699,2429)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...82){\makebox(0,0)[b]{$C$ }}
\put(1887,982){\makebox(0,0)[b]{$B$ }}
\end{picture}](img20.gif)
![\begin{picture}(3699,2429)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...box(0,0)[b]{$\frac{1}{2}$ }}
\put(1887,1207){\ellipse{2400}{2400}}
\end{picture}](img21.gif)
![\begin{picture}(3699,2429)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...807){\makebox(0,0)[b]{$F$ }}
\put(1887,1207){\ellipse{2400}{2400}}
\end{picture}](img23.gif)
![\begin{picture}(3699,2429)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...982){\makebox(0,0)[b]{$G$ }}
\put(1887,1207){\ellipse{2400}{2400}}
\end{picture}](img24.gif)
![\begin{picture}(3699,2542)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...\makebox(0,0)[b]{$\theta$ }}
\put(1887,1207){\ellipse{2400}{2400}}
\end{picture}](img25.gif)
![\begin{picture}(3699,2542)(0,-10)
\put(687,1207){\blacken\ellipse{50}{50}}
\put(...
...392){\makebox(0,0)[b]{$H$ }}
\put(1887,1207){\ellipse{2400}{2400}}
\end{picture}](img29.gif)