Computing a Set of Values of EXP(x)

Problem Statement

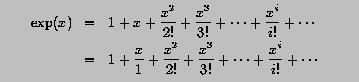
In a previous example we have discussed the way of using infinite series for computing the exponential function EXP(x). The exponential function, EXP(x), is usually defined to be the sum of the following infinite series:

Write a program that reads in an initial value Begin, a final value End and a step size Step, and computes the exponential function value at Begin, Begin+Step, Begin+2*Step, ...

Solution

! --------------------------------------------------------------
! This program computes exp(x) for a range of x.  The range
! is in the form of beginning value, final value and step size.
! For each value in this range, the infinite series of exp(x)
! is used to compute exp(x) up to a tolerance of 0.00001.
! This program display the value of x, the exp(x) from infinite
! series, the exp(x) from Fortran's intrinsic function exp(x),
! the absolute error, and the relative error.
! --------------------------------------------------------------

PROGRAM  Exponential
   IMPLICIT  NONE

   INTEGER         :: Count             ! term count
   REAL            :: Term              ! a term
   REAL            :: Sum               ! the sum of series
   REAL            :: X                 ! running value
   REAL            :: ExpX              ! EXP(X)
   REAL            :: Begin, End, Step  ! control values
   REAL, PARAMETER :: Tolerance = 0.00001    ! tolerance

   WRITE(*,*)  'Initial, Final and Step please --> '
   READ(*,*)   Begin, End, Step

   X = Begin                            ! X starts with the beginning value
   DO
      IF (X > End)  EXIT                ! if X is > the final value, EXIT
      Count = 1                         ! the first term is 1 and counted
      Sum   = 1.0                       ! thus, the sum starts with 1
      Term  = X                         ! the second term is x
      ExpX  = EXP(X)                    ! the exp(x) from Fortran's EXP()
      DO                                ! for each term
         IF (ABS(Term) < Tolerance)  EXIT ! if too small, exit
         Sum   = Sum + Term             !   otherwise, add to sum
         Count = Count + 1              !   count indicates the next term
         Term  = Term * (X / Count)     !   compute the value of next term
      END DO

      WRITE(*,*)  X, Sum, ExpX, ABS(Sum-ExpX), ABS((Sum-ExpX)/ExpX)

      X = X + Step
   END DO

END PROGRAM  Exponential

Click here to download this program.

Program Input and Output

If the input for Begin, End and Step are -1.0, 1.0 and 0.1, the program would generate the following output.

 Initial, Final and Step please -->
 -1.,  0.367881894,  0.36787945,  2.443790436E-6,  6.642911103E-6
 -0.899999976,  0.406570643,  0.40656966,  9.834766388E-7,  2.41896214E-6
 -0.799999952,  0.449325144,  0.449328989,  3.844499588E-6,  8.556090506E-6
 -0.699999928,  0.496584028,  0.496585339,  1.311302185E-6,  2.640638058E-6
 -0.599999905,  0.5488168,  0.548811674,  5.125999451E-6,  9.340179531E-6
 -0.499999911,  0.606532216,  0.606530726,  1.490116119E-6,  2.456785978E-6
 -0.399999917,  0.670314729,  0.670320094,  5.36441803E-6,  8.002770301E-6
 -0.299999923,  0.740817249,  0.740818262,  1.013278961E-6,  1.367783398E-6
 -0.199999928,  0.818733335,  0.818730831,  2.503395081E-6,  3.05765343E-6
 -9.999992698E-2,  0.904833436,  0.904837489,  4.053115845E-6,  4.479385552E-6
 7.450580597E-8,  1.,  1.00000012,  1.192092896E-7,  1.192092753E-7
 0.100000076,  1.10516667,  1.10517097,  4.291534424E-6,  3.883140835E-6
 0.200000077,  1.22140002,  1.22140288,  2.861022949E-6,  2.342407242E-6
 0.300000072,  1.34985793,  1.34985888,  9.536743164E-7,  7.064992928E-7
 0.400000066,  1.4918189,  1.49182475,  5.841255188E-6,  3.915510206E-6
 0.50000006,  1.64871967,  1.64872134,  1.668930054E-6,  1.012257258E-6
 0.600000083,  1.82211316,  1.822119,  5.841255188E-6,  3.205748499E-6
 0.700000107,  2.01375127,  2.01375294,  1.668930054E-6,  8.287660194E-7
 0.800000131,  2.22553682,  2.22554111,  4.291534424E-6,  1.928310667E-6
 0.900000155,  2.45960236,  2.45960355,  1.192092896E-6,  4.846687034E-7

The first column shows the data values (i.e., -1.0, -0.9, ..., 1.0), the second is the values from using infinite series with a tolerance value 0.00001, the third column contains the values from Fortran's intrinsic function EXP(), the forth column has the absolute errors, and the fifth column has the relative errors.

Let S be the sum computed using infinite series and exp(x) be the result from Fortran's intrinsic function. Then, the absolute error and relative error are defined as follows:

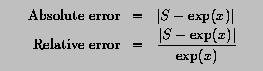
You may find out that the value for X are not -1.0, -0.9, -0.8, ..., 0.0, 0.1, 0.2, ..., 0.9 and 1.0. It contains errors. For example, the last value should be 1.0 instead of 0.900000155. This is a problem of precision being not high enough. See the KIND attribute in a later chapter.

Discussion

For the computation using infinite series, see a previous example for the details.
Since the data points are Begin, Begin+Step, Begin+2*Step and so on, it is simply a DO-loop as follows:
```
X = Begin
DO
   IF (X > End)  EXIT
     ... compute EXP(X) here ...
   X = X + Step
END DO
```
Inserting the computation part into the place "... computing EXP(X) here ..." gives the program shown above.