
The hodograph of a curve is actually its first derivative. The hodograph (i.e., first derivative) of a Bézier (resp., B-spline) curve of degree p is a Bézier (resp., B-spline) curve of degree p-1 whose control points can be computed easily from the given control points. As a result, computing the second derivative of a Bézier or a B-spline curve is a simple task, because one can construct the control points of the hodograph and then construct the hodograph of the hodograph. In fact, it is not difficult to fine a formula for higher order derivatives.
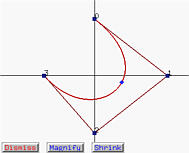
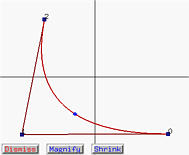
Selecting Hodograph (First Derivative) and Second Derivative will open the hodograph and second derivative windows, respectively. Select Dismiss to close the window. These windows have two more buttons. Magnify and Shrink can be used to zoom in and zoom out with respect to the coordinate origin. If a curve has many control points, it is possible that some control points in the hodograph and second derivative windows are too populated to be shown clearly. Thus, Magnify and Shrink are useful in this and other cases.
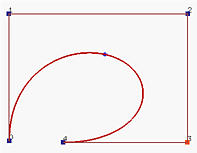
In the following, the left figure is a Bézier curve of degree 4 with u = 0.42. The middle one is the hodograph window and the right one is the second derivative window. In all windows, the control points are clearly shown. As u moves on the given curve p(u), the points on p'(u) and p''(u) are shown on-the-fly. The tangent (resp., second derivative) vector is the vector from the coordinate origin to p'(u) (resp., p''(u)).



However, rational Bézier and NURBS curves do not have such an elegant property. Their hodograph and second derivative curves are no more rational Bézier and NURBS curves and as a result no control points are shown in the hodograph and second derivative windows.
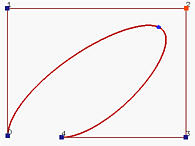

The above shows the hodograph and second derivative of a rational Bézier curve. In this case, Shrink is needed to bring the hodograph and second derivative curves into the window area.
Further discussion can be found in The First Derivative (Hodograph) and Second Derivative.