
Degree elevation increases the degree of a curve without changing the shape of the curve. Together with knot insertion, they provide two frequently used techniques to make to curves compatible. Two curves are compatible if they are of the same type and have the same number of control points, the same number of knots and the same degree. Due to the fundamental identify, if the degree and the number of knots are known, the number of control points are determined. As a result, if two curves of the same type have the same number of knots and the same degree, they much have the same number of control points. Therefore, knot insertion is used to make the knot vectors identical and degree elevation makes the curves of the same degree.
Select Techniques followed by Degree Elevation. The degree of the current curve will be increased by one. To increase the degree by more than one, repeat this process.
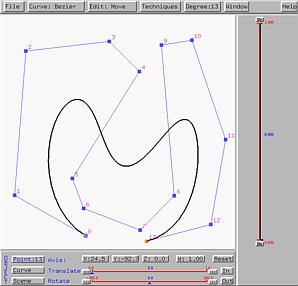
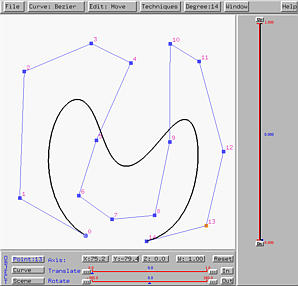
The left figure below is a Bézier curve of degree 14. After performing degree elevation increasing its degree to 14, we have the right figure below. It now has 15 control points. Note that the shape of the Bézier curve does not change.


Degree elevation for B-spline and NURBS curves is performed by subdividing the curve into Bézier curve segments, increasing the degree of each Bézier segment, and combining them together back to a single B-spline and NURBS curve. So, increasing the degree of a Bézier curve is an important procedure.
The following left figure is a NURBS curve of degree 4 defined by 8 control points. After degree elevation, we have the right figure. It is of degree 5 defined by 12 control points.
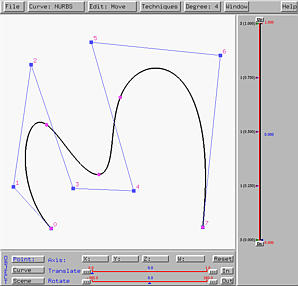
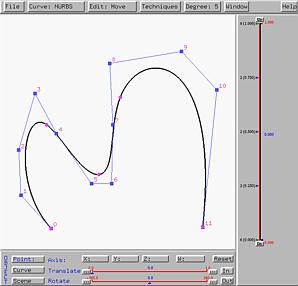
If you are careful, you may have already found out that degree elevation will cause the set of control points modified "globally". More precisely, unlike knot insertion, all control points, except for the two endpoints, are replaced with new ones.