Boolean Operations

We have not used object { } previously. We shall start using now because spheres, boxes and cones are shapes and are also objects. Moreover, Boolean operations union, difference and intersection create objects rather than shapes.

When using Boolean operations, each object must have inside (i.e., interior) and outside (i.e., exterior). It is easy to understand the inside and outside of spheres, cones and tori; but, plans could be a problem. Recall that normal vectors of a surface always point outward. In defining a plane, its normal vector indicates the exterior. For example, the exterior of plane plane { y, 0 } is the half-space above the xz-plane and its interior is the half-space below the xz-plane.

We only use POV-Ray's union { }, intersection { } and difference { }. POV-Ray also supports another type union called merge { }, which could be very useful when constructing transparent objects. Older version of POV-Ray even supports composite { }. But, for our purpose, union { }, intersect { } and difference { } are sufficient.

Boolean Operator -- union

Union { } has the following syntax:

union {
     shape/object 1
     shape/object 2
         ......
     shape/object n
}

These objects or shapes will be unioned becoming a single object, which you can translate, rotate and scale. Each of these objects or shapes can have their own pigment { } and/or finish { }. Those without will inherit from the one given to this union { } later on.

#declare  TwoSphere =
               union {
                    sphere {  x, 1.3  }
                    sphere { -x, 1.3 pigment { color Yellow } }
               }

object {
     TwoSphere
     pigment {
          color  Red
     }
     finish {
          phong  1
          ambient 0.2
     }
}

The above example defines a union of two spheres. The right sphere does not have any texture specification (i.e., pigment, normal and finish), while the left sphere only has pigment. When this union is used in an object, which has red color and phong and ambient value, these texture information will be inherited by the right sphere; however, since the left sphere has already had texture information, the left sphere will use its own. Therefore, in the raytraced image below, the yellow sphere looks dull since it does not inherit phong and ambient from the object.

An Example

Let us design a toy which consists of a hat (cone), a head (sphere), an arm (cylinder) and a body (cylinder). Its dimensions are shown below left and raytraced result is shown below right.

The following are POV-Ray definitions:

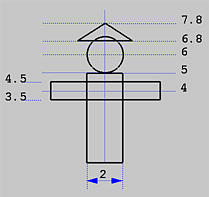
#declare  Head =
               sphere {
                    < 0, 6, 0 >, 1
               }

#declare  Hat =
               cone {
                    < 0, 6.8, 0 >, 1.5, < 0, 7.8, 0 >, 0
               }

#declare  Body =
               cylinder {
                    < 0, 0, 0 >, < 0, 5, 0 >, 1
               }

#declare  Arms =
               cylinder {
                    < -3, 4, 0 >, < 3, 4, 0 > 0.5
               }

#declare  Toy =
               union {
                    object { Head }
                    object { Hat }
                    object { Body }
                    object { Arms }
               }

The above declares an identifier Toy which can be used as a single unit. In the following, we put four of them into our scene, facing each other. Note that all of them carry a texture Chrome_Metal which is declared in a header file textures.inc.

object {
     Toy                      // on positive x-axis
     texture {
          Chrome_Metal
     }
     rotate      90*y
     translate   4.5*x
}

object {
     Toy                      // on positive y-axis
     texture {
          Chrome_Metal
     }
     translate   4.5*z
}

object {
     Toy                      // on negative x-axis
     texture {
          Chrome_Metal
     }
     rotate      90*y
     translate   -4.5*x
}

object {
     Toy                      // on negative z-axis
     texture {
          Chrome_Metal
     }
     translate   -4.5*z
}

Here is the raytraced result:

Clink here to download a complete scene file.

Boolean Operator -- intersection

Intersection operator keeps the common part of all involved objects. It has a syntax as follows:

intersection {
     shape/object 1
     shape/object 2
         ......
     shape/object n
}

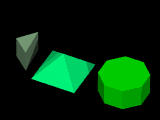
Let us design a prism, a pyramid and an octagonal cylinder as shown in the right figure below.

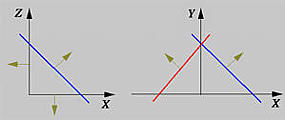
An unbounded prism can be constructed as the intersection of three planes as follows:

#declare  Prism =
          intersection {
               plane { < 1, 0, 1 >, sqrt(2)/2 }
               plane { -x, 0 }
               plane { -z, 0 }
               object { BoundingBox }
          }

The object BoundingBox is a box for extracting the part of an object between y = 0 and y = 1. This is shown in the left figure above with normal vectors in light orange color. Since the exterior of a plane is in its normal's direction, if the three normal vectors change their directions, the intersection is empty.

An unbounded pyramid is the intersection of four planes:

#declare  Pyramid =
          intersection {
               plane { < 1, 1, 0 >, sqrt(2)/2 }
               plane { < 1, 1, 0 >, sqrt(2)/2 rotate 90*y}
               plane { < 1, 1, 0 >, sqrt(2)/2 rotate 180*y}
               plane { < 1, 1, 0 >, sqrt(2)/2 rotate 270*y}
               object { BoundingBox }
          }

The first plane is perpendicular to the xy-plane and has its normal vector pointing in the direction of < 1, 1, 0 >. Then, this plane is rotated 90 degree about the y-axis, generating a second one. The original plane is rotated 180 degree and 270 degree to obtain the other two planes. All four planes contain the point < 0, 1, 0 >. Since the intersection is unbounded, object BoundingBox is used again to extract the part of y >= 0.

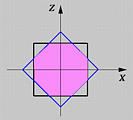
The octagonal cylinder can be constructed as the intersection of eight planes. But, due to symmetry, this can be simplified a little as follows:

#declare  Infinite_Block =
          intersection {
               plane { x, 1 }
               plane { x, 1 rotate 90*y }
               plane { x, 1 rotate 180*y }
               plane { x, 1 rotate 270*y }
          }

#declare  AngularCylinder =
          intersection {
               object { Infinite_Block }
               object { Infinite_Block rotate 45*y }
               object { BoundingBox }
          }

First, an unbounded box is constructed as the intersection of four planes, all of them perpendicular to the xz-plane (i.e., the black square shown in the middle figure). This object is called Infinite_Block above. Now we have four corners. To generate four more, rotate Infinite_Block 45 degree (i.e., the blue square shown in the figure) and intersect the result with the original. The result is an octagonal cylinder called AngularCylinder. Again, BoundingBox is used to extract the part between y = 0 and y = 1.

Click here to download a complete scene file.

Boolean Operator -- difference

The difference operator is used to remove some part of an object. It has the following syntax:

difference {
     shape/object 1
     shape/object 2
         ......
     shape/object n
}

Those part in the second to the last object/shape will be removed from the first object/shape.

Let us design an ash tray as shown in the right figure below.

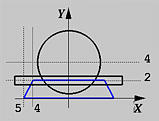
The base of this ash tray is a cone shown in blue in the left figure above. The following is its POV-Ray definition:

#declare  Cone =
               cone { < 0, 0, 0 >, 5, < 0, 2, 0 >, 4 }

To dig a "hole" in the middle, we can subtract a sphere from the cone. Of course, this sphere cannot penetrate the cone:

#declare  Sphere =
               sphere { < 0, 4, 0 >, 3.5 }

Then, to complete the design, we need to subtract two cylinders from the about result:

#declare  Cylinder =
               cylinder { < -6, 2, 0 >, < 6, 2, 0 >, 0.5 }

#declare  Tray =
               difference {
                    object { Cone }
                    object { Sphere }
                    object { Cylinder }
                    object { Cylinder  rotate 90*y }
               }

Note that in the above, the second cylinder is obtained from rotating the object Cylinder 90 degree about the y-axis.

Click here to download a complete scene file.

Very Important!!!!!

Since POV-Ray does not implement regularized Boolean operations (i.e., union, intersection and difference are done as conventional set operations), in a CSG expression A - B the object B should have a larger dimension to avoid lower dimension components to appear in the result. For example, suppose we want to punch a hole from a box in the y-direction with the following:

#declare Box_with_Hole = difference { box { < -1, -1, -1 >, < 1, 1, 1 > } box { < -0.5, -1, -0.5 >, < 0.5, 1, 0.5 > } }

It may not work and the result could be a "solid" box. The reason is that the top and bottom faces of the smaller box match with those of the larger one exactly. Increasing the heights usually overcomes the problem:

#declare Box_with_Hole = difference { box { < -1, -1, -1 >, < 1, 1, 1 > } box { < -0.5, -1.1, -0.5 >, < 0.5, 1.1, 0.5 > } }

In the above, the height of the smaller box runs from -1.1 to 1.1, which are slightly larger than the height of the larger box.