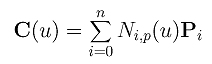

Given n + 1 control points P0, P1, ..., Pn and a knot vector U = { u0, u1, ..., um }, the B-spline curve of degree p defined by these control points and knot vector U is
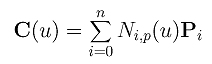
where Ni,p(u)'s are B-spline basis functions of degree p. The form of a B-spline curve is very similar to that of a Bézier curve. Unlike a Bézier curve, a B-spline curve involves more information, namely: a set of n+1 control points, a knot vector of m+1 knots, and a degree p. Note that n, m and p must satisfy m = n + p + 1. More precisely, if we want to define a B-spline curve of degree p with n + 1 control points, we have to supply n + p + 2 knots u0, u1, ..., un+p+1. On the other hand, if a knot vector of m + 1 knots and n + 1 control points are given, the degree of the B-spline curve is p = m - n - 1. The point on the curve that corresponds to a knot ui, C(ui), is referred to as a knot point. Hence, the knot points divide a B-spline curve into curve segments, each of which is defined on a knot span. We shall show that these curve segments are all Bézier curve of degree p on the curve subdivision page.
Although Ni,p(u) looks like Bn,i(u), the degree of a B-spline basis function is an input, while the degree of a Bézier basis function depends on the number of control points. To change the shape of a B-spline curve, one can modify one or more of these control parameters: the positions of control points, the positions of knots, and the degree of the curve.
If the knot vector does not have any particular structure, the generated curve will not touch the first and last legs of the control polyline as shown in the left figure below. This type of B-spline curves is called open B-spline curves. We may want to clamp the curve so that it is tangent to the first and the last legs at the first and last control points, respectively, as a Bézier curve does. To do so, the first knot and the last knot must be of multiplicity p+1. This will generate the so-called clamped B-spline curves. See the middle figure below. By repeating some knots and control points, the generated curve can be a closed one. In this case, the start and the end of the generated curve join together forming a closed loop as shown in the right figure below. In this note, we shall use clamped curve.



The above figures have n+1 control points (n=9) and p = 3. Then, m must be 13 so that the knot vector has 14 knots. To have the clamped effect, the first p+1 = 4 and the last 4 knots must be identical. The remaining 14 - (4 + 4) = 6 knots can be anywhere in the domain. In fact, the curve is generated with knot vector U = { 0, 0, 0, 0, 0.14, 0.28, 0.42, 0.57, 0.71, 0.85, 1, 1, 1, 1 }. Note that except for the first four and last four knots, the middle ones are almost uniformly spaced. The figures also show the corresponding curve segment on each knot span. In fact, the little triangles are the knot points.
