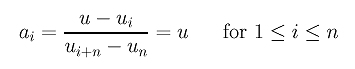

Because a Bézier curve is a B-spline curve in a special form and because de Boor's algorithm works very similar to de Casteljau's algorithm, we expect that the latter may be a special case of the former. This indeed is the case.
Suppose we have a B-spline curve C(u) of degree n defined by n+1 control points P0, ..., Pn and a knot vector of p+1 0's followed by p+1 1's. We discussed on a previous page that C(u) is actually a Bézier curve of degree n.
Consider the computation steps of de Boor's algorithm. We already know C(0) = P0 and C(1) = Pn. What we need to show is that de Boor's algorithm and de Casteljau's algorithm act the same way and compute the same result for every u. Let the knots be u0 = u1 = ... = un = 0 and un+1 = un+2 = ... = u2n+1 = 1. Given any u in (0,1), it is in [un, un+1). Consequently, the control points that involve in the knot insertion computation are Pn, ..., Pn-n = P0, and the intervals used for calculating the ai's are [un, un+n) = [0,1), [un-1, un+n-1) = [0,1), ..., and [un-n+1, un+1) = [0,1). Therefore, for each i, we have
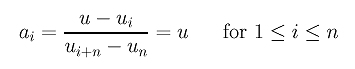
Since each leg is divided with a ratio of ai:1-ai, the above expression shows that in this special case the dividing ratio is all the same and is equal to u:1-u. Thus, the first knot insertion in de Boor's algorithm computes exactly the first column in de Casteljau's algorithm.
A similar argument shows that the dividing ratio in all subsequent insertion steps is also equal to u:1-u. Consequently, in this special case, the computation steps of de Boor's algorithm are exactly identical to the corresponding steps of de Casteljau's algorithm. Therefore, de Boor's algorithm reduces to de Casteljau's algorithm when the knot vector has only two knots of multiplicity n+1.