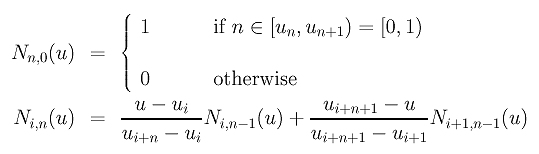

If we have 2n+2 knots u0 = u1 = ... = un = 0 and un+1 = un+2 = ... = u2n+1 = 1 (i.e., the first n+1 being 0 and the next n+1 being 1), what are the B-spline basis functions of degree n?
Since every u is in [0,1] = [un, un+1], the non-zero basis functions of degree n are: N0,n(u), N1,n(u), ..., Nn,n(u). Recall the definition of B-spline basis functions as follows:
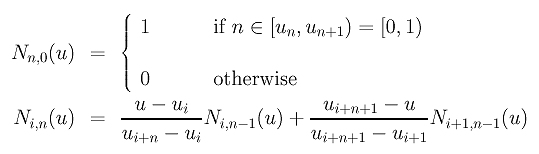
Since the only non-zero basis function of degree 0 is Nn,0(u), the index i can only be in the range of 0 and n. Therefore, the ui's are zero and ui+n's and ui+n+1's are 1. Consequently, the second equation above can be rewritten as follows:
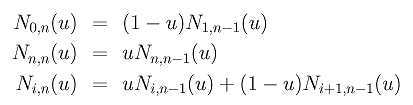
If we organize the computation of N0,n(u), N1,n(u), ..., Nn,n(u) in a triangular form as discussed on the previous page, we have the following diagram. In this diagram, each north-east (resp., south-east) bound arrow means multiplying 1-u (resp., u) to the term at the tail of the arrow. Note that there are n stages in the computation, one for obtaining each column. Therefore, the contribution of Nn,0(u) to N0,n(u) is (1-u)n, and the contribution of Nn,0(u) to Nn,n(u) is un.
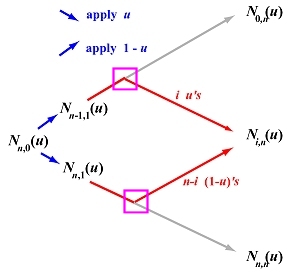
Now, consider the computation of a general term Ni,n(u). The contribution of Nn,0(u) to the computation of Ni,n(u) can be determined by the "path-counting" technique that was used to show the correctness of de Casteljau's algorithm and in the computation of higher derivatives of a Bézier curve. Each path going from Nn,0(u) to Ni,n(u) encounters n arrows of which i are south-east bound and n-i are north-east bound. Those north-east (resp., south-east) bound arrows mean multiply the term at the tail by 1-u (resp., u). Therefore, the contribution of Nn,0(u) to Ni,n(u) along a single path is ui(1-u)n-i. The total number of paths from Nn,0(u) to Ni,n(u) is C(n,i). More precisely, the number of paths is equal to the number of different ways of placing i south-east bound arrows in n positions. The remaining n-i positions are filled with north-east bound arrows. This n arrows precisely describe a single path from Nn,0(u) to Ni,n(u). Since each path contributes ui(1-u)n-i to the computation and since there are C(n,i) paths, the total contribution of Nn,0(u) to Ni,n(u) is
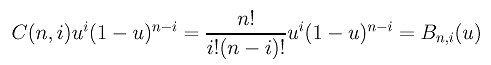
This is exactly the i-th Bézier basis function of degree n. Therefore, we have the following conclusion:
| If the first (resp., last) n+1 knots are equal to 0 (resp., 1), then the i-th B-spline basis function of degree n is identical to the i-th Bézier basis function for all i in the range of 0 and n. Hence, the Bézier basis functions are special cases of B-spline basis functions, and Bézier curves are special cases of B-spline curves. |