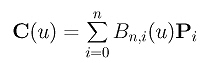

We shall establish the correctness of the subdivision algorithm. It requires some tedious, but simple, calculations. Suppose the given Bézier curve of degree n is defined by n+1 control points P0, P1, ..., Pn. Suppose further the curve is subdivided at a fixed u in [0,1]. The subdivision algorithm states that the curve segment on [0,u] is defined by points P00=P0, P10, P20, ...., Pn0. To establish the correctness of the subdivision algorithm, our strategy is (1) find the Bézier curve of degree n defined by control points P00=P0, P10, P20, ...., Pn0 and (2) verify that this curve is the given curve restricted on domain [0,u]. The same technique applies to the second curve segment on [u,1].
Let the original curve be
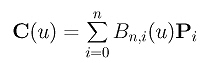
According to the observations discussed on the de Casteljau's algorithm page, we know that point Pk0 is computed from control points P0, P1, ..., Pk at the fixed value u:
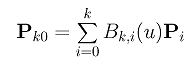
The Bézier curve of degree n defined by P00=P0, P10, P20, ...., Pn0 is
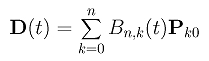
where t is in [0,1]. Note that we use a different parameter value t to avoid confusion. Note also that the domain of this curve is [0,u] rather than [0,1]. This can be done easily with a simple change of parameter. We will do this at the end of this proof. Plugging Pk0 into the curve D(t), we have
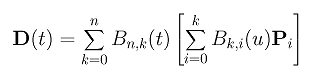
Therefore, the curve D(t) is still represented by the original control points P0, P1, ..., Pn. If we can figure out the coefficient of each Pi, we will have a proof! Consider point Ph. When k is greater than or equal to h, the term Bk,h(u) is the coefficient of Ph. Therefore, the coefficient of Ph in the curve D(u) is:
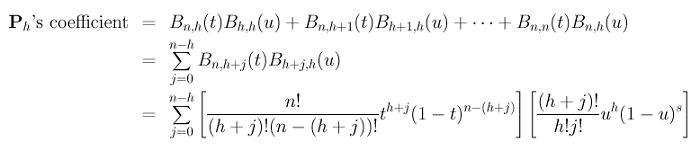
Terms (tu)h, n! and j! can be moved to the outside of the summation:
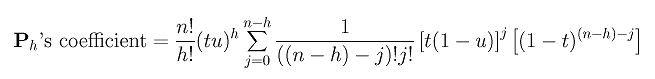
We are almost there because we have (tu)h, n! and j, the missing part is a (n-h)!. So, let us multiply (n-h)! to each term in the summation and divide the outside term by (n-h)!. This yields:
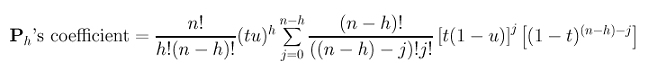
Recall the following binomial expansion of (a+b)m:
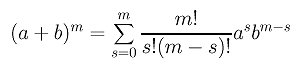
The summation can be simplified with the above binomial expansion formula to the following:
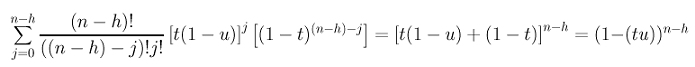
Hence, the coefficient of Ph is:
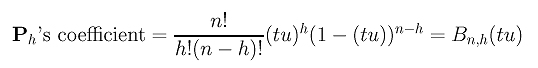
The relationship between the original curve C(u) and the subdivision curve on [0,u] is shown below:
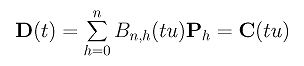
This means that when t traces the curve D(u) on [0,1], tu traces the original curve C(u) in the interval [0,u]. Moreover, these two components are identical, and, as a result, curve D(t) is the curve segment of C(u) on [0,u]. This establishes the correctness of the subdivision algorithm.