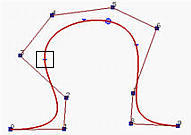
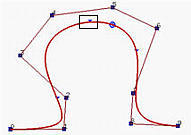
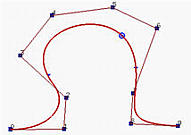

Because a B-spline curve is a composition of curve segments, each of which is defined on a knot span, modifying the position of one or more knots will change the association between curve segments and knot spans and hence change the shape of the curve.
The following figures depict the effect of modifying a single knot. It is a B-spline of degree 6 with 17 knots with first seven and last seven clamped at the end points, while the knots in the middle are 0.25, 0.5 and 0.75. The initial curve is shown in the left. If knot 0.25 is moved to 0.1, the shape of the curve changes and the original p(0.25) moves downward to a new position. If knot 0.5 is moved to 0.1 so that knot 0.1 becomes a double knot (with multiplicity 2), the shape of curve moves to the left; but p(0.1) is moved upward to a position near to the original point (i.e., the original p(0.25)). The result is shown in the right figure. Moreover, even though we have a double knot at 0.1 and a third knot at 0.75 that unevenly subdivide the domain [0,1] into three knot spans, the B-spline curve is more or less evenly subdivided by their corresponding points.



However, practical experience shows that modifying knot positions is neither predictable nor satisfactory. More precisely, because it is not clear how the shape of a B-spline curve will respond to the change of the knot vector, modifying the shape of B-spline curve by changing knots is usually unsatisfactory and difficult to achieve the desired goal.

Suppose a knot has multiplicity p-k, there will be k+1 non-zero basis functions at this knot and hence the corresponding point on the curve lies in the convex hull defined by the control points that correspond to these non-zero basis functions. If k = p - 1, there are two non-zero functions and the corresponding convex hull is a line segment.
If k = p, there is only one non-zero function at this knot and hence there is only one control point has non-zero coefficient. As a result, the curve passes through this point!
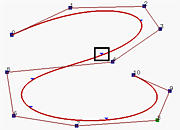
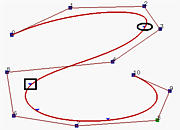
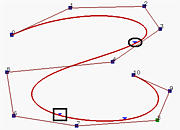
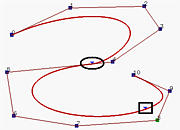

In the first figure above, which shows a B-spline curve of degree 5, the knot that corresponds to the curve dividing point (marked with a rectangle) is moved to its previous knot, creating a knot of multiplicity two. The result is the second figure, which does not show much difference from the original. Then, the next knot (marked with a rectangle) is moved to the resulting knot (marked with an ellipse) again, creating a knot of multiplicity three. This is the third figure. The resulting curve moves towards a leg of the control polyline. Moving one more knot creates a new knot of multiplicity four. This forces the corresponding point (marked with an ellipse) lies on a leg. Finally, the only remaining knot is moved to combined with the other knot. Since its multiplicity is five and p=5, there is only one non-zero coefficient and hence forces the curve to pass that control point. As shown in the fifth figure, that control point is p5.