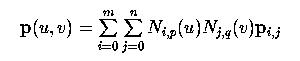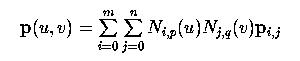B-spline Surfaces: Important Properties

Several important properties of B-spline surfaces are listed here. These properties can be proved easily by applying the same techniques used for Bézier curves. Please compare these important properties with those of B-spline curves'. Please recall that the equation of a B-spline surface is the following

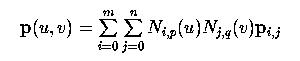
where the degrees in the u- and v-directions are p and q, respectively, and there are m+1 rows and n+1 columns of control points.

• Nonnegativity: N_i,p(u) N_j,q(v) is nonnegative for all p, q, i, j and u and v in the range of 0 and 1.
  This is obvious.

• Partition of Unity: The sum of all N_i,p(u) N_j,q(v) is 1 for all u and v in the range of 0 and 1.
  More precisely, this means for any pair of u and v in the range of 0 and 1, the following holds:
  

• Strong Convex Hull Property: if (u,v) is in [u_i,u_i+1) x [v_j,v_j+1), then p(u,v) lies in the convex hull defined by control points p_h,k, where i-p <= h <= i and j-q <= k <= j.
  This strong convex hull property for B-spline surfaces follows directly from the strong convex hull property for B-spline curves. For the u-direction, if u is in [u_i,u_i+1), then there are at most p+1 non-zero basis functions, namely, N_i,p(u), N_i-1,p(u), ..., and N_i-p,p(u). Thus, only the control points on row i-p to row i have non-zero basis functions in the u-direction. Similarly, if v is in [v_j,v_j+1), there are at most q+1 non-zero basis functions on this knot span, namely N_j,q(v), N_j-1,q(v), ..., and N_j-q,q(v). Thus, only the control points on column j-q to column j have non-zero basis functions in the v-direction. Combining these two facts together, only the control points in the range of row i-p to row i and column j-q to q have non-zero basis functions. Since these basis functions are nonnegative and their sum is one (i.e., the partition of unity property), p(u,v) lies in the convex hull defined by these control points.

  As a result, the surface patch defined on rectangle [u_i,u_i+1) x [v_j,v_j+1) lies completely in the same convex hull.

• Local Modification Scheme: N_i,p(u)N_j,q(v) is zero if (u,v) is outside of the rectangle [u_i,u_i+p+1) x [v_j,v_j+q+1)
  From the local modification scheme property, we know that in the u-direction N_i,p(u) is non-zero on [u_i,u_i+p+1) and zero elsewhere. The local modification scheme property of B-spline surfaces follows directly from the curve case. If control point p_3,2 is moved to a new location, the following figures show that only the neighboring area on the surface of the moved control point changes shape and elsewhere is unchanged.
  

• p(u,v) is C^p-s (resp., C^q-t) continuous in the u (resp., v) direction if u (resp., v) is a knot of multiplicity s (resp., t).

• Affine Invariance
  This means that to apply an affine transformation to a B-spline surface one can apply the transformation to all control points and the surface defined by the transformed control points is identical to the one obtained by applying the same transformation to the surface's equation.

• Variation Diminishing Property:
  No such thing exists for surfaces.

• If m = p, n = q, and U = { 0, 0, ..., 0, 1, 1, ...., 1 }, then a B-spline surface becomes a Bézier surface.